|
Abstract TECHNOLOGY OF SEARCHING OPTIMUM GYMNASTIC EXERCISES’ TECHNIQUE IN IMITATING MATHEMATICAL MODELLING HUMAN MOVEMENTS V.I. Zagrevsky, Dr. Hab., professor D.A. Lavshuk The Mogilyov state A.A.Kuleshov’s university, Mogilyov, Byelorussia O.I. Zagrevsky, Dr. Hab., professor Tomsk state university, Tomsk Key words: biomechanical synthesis, mathematical model of movements, imitating modelling, optimum control, sports exercises technique. The movements’ synthesis developed by the authors on the basis of the method of global local variations in managements’ space allows to create a sports exercises’ technique with a beforehand predicted change of biosystem’s configuration. The analysis of the pedagogical experiment’s results has shown, that the optimum technique of exercises, preliminary constructed in the computing experiment, promotes their effective mastering on the higher technical level and the reduction of time used for the process of learning.
|

ТЕХНОЛОГИЯ ПОИСКА ОПТИМАЛЬНОЙ ТЕХНИКИ ГИМНАСТИЧЕСКИХ УПРАЖНЕНИЙ В ИМИТАЦИОННОМ МАТЕМАТИЧЕСКОМ МОДЕЛИРОВАНИИ ДВИЖЕНИЙ ЧЕЛОВЕКА
Доктор педагогических наук, профессор
О. И. Загревский Ключевые слова: биомеханический синтез, математическая модель движений, имитационное моделирование, оптимальное управление, техника спортивных упражнений. Введение. Современный спорт характеризуется высоким уровнем спортивных достижений и все возрастающей конкуренцией, что обусловливает поиск и разработку новых технологий в системе подготовки спортсменов высокой квалификации. В частности, в видах спорта, связанных с искусством движений (например, гимнастика, акробатика, прыжки в воду), актуален вопрос совершенствования технической подготовленности спортсменов. На наш взгляд, одним из перспективных направлений ее эффективного совершенствования у спортсменов является метод прогнозирования оптимальной техники спортивных упражнений. Двигательные действия человека, в частности спортсмена, представляют собой сложную биомеханическую структуру [1]. Возможности прогнозирования рациональной техники спортивных упражнений для конкретного исполнителя и построения биомеханически целесообразных и эффективных структур новых двигательных действий крайне ограниченны. В настоящее время обучение технике спортивных упражнений строится на основе теоретических сведений об общих биомеханических закономерностях структурной группы движений, не учитывающих индивидуальных антропометрических особенностей спортсменов. А на практике совершенствование техники спортивных упражнений осуществляется эмпирически, методом проб и ошибок [1]. Предварительное теоретическое обоснование оптимальных вариантов построения движений для конкретных исполнителей не проводится ввиду отсутствия методики синтеза и оптимизации двигательных действий спортсмена. Единственным методом исследований, позволяющим синтезировать технику движений спортсмена не в логической, а в количественной форме, является метод имитационного моделирования на персональном компьютере (ПК) [2]. В качестве гипотезы исследования нами выдвинут тезис о том, что ПК можно использовать в качестве не только вычислительного инструмента, но и конструктора оптимальной техники гимнастических упражнений. В соответствии с гипотезой были сформулированы следующие задачи исследования: 1. На кинематическом уровне программного управления разработать конструктивную математическую модель синтеза движений спортсмена, позволяющую адекватно реализовывать двигательные задачи кинематической структуры исследуемого упражнения на всей траектории биомеханической системы. 2. Разработать компьютерную технологию поиска оптимального управления движениями биомеханических систем с целью построения оптимальной техники соревновательных упражнений с учетом ограничений, накладываемых на кинематические и динамические ресурсы исполнителя. 3. Проверить в педагогическом эксперименте целесообразность и эффективность использования в учебно-тренировочном процессе программного комплекса, реализующего технологию компьютерного поиска оптимальной техники соревновательных упражнений. Методы и организация исследования. В работе использовались следующие методы: видеосъемка спортивных упражнений, компьютерная обработка видеоматериалов регистрации движений спортсменов и построение видеограмм упражнений на ПК, экспериментально-аналитический метод определения геометрии массы тела человека, аналитический расчет кинематических и динамических характеристик движения, механико-математический метод моделирования динамических систем, математические методы оптимизации движения управляемых биомеханических систем, вычислительные эксперименты на ПК, педагогический эксперимент, методы математической статистики для обработки результатов вычислительного и педагогического экспериментов. Практически все вышеперечисленные методы в достаточной степени освещены в специальной литературе. Исключениями являются механико-математический метод моделирования динамических систем и математические методы оптимизации движения управляемых биомеханических систем. Последние изложены фрагментарно, поэтому опишем их подробнее. Мы ограничились исследованием многозвенных неразветвленных биомеханических систем. Рассмотрим кинематическую схему модели опорно-двигательного аппарата тела человека на примере трехзвенной биомеханической системы (рис. 1), в которой руки - первое звено, туловище с головой - второе, ноги - третье. Расположим кисти рук спортсмена в начале не подвижной системы координат Оху, а ее, в свою очередь, совместим с торцом грифа перекладины. Введем в кинематическую схему модели обозначения: N - количество звеньев модели; Li - длина i-го звена; Si - расстояние от оси вращения (гриф перекладины) до центра масс i-го звена;
В математической форме учет управляющих воз действий мышечных сил на биомеханику движения заключается во введении в правую часть уравнений естественного движения управляющих моментов мышечных сил в суставах (Mi), записываемых для i-го уравнения системы в виде алгебраической суммы слагаемых MI - MI +1, где MI +1 = 0, если i < N и MI +1 = 0, если i=N.
Рис. 1. Кинематическая схема трехзвенной мо дели опорно-двигательного аппарата тела человека Для N-звенной неразветвленной биомеханической системы при описанных выше обозначениях уравнения имеют следующий вид:
где А - элементы матрицы, определяемые масс инерционными характеристиками исполнителя, Y - обобщенные силы, определяемые как момент силы тяжести для i-го звена относительно опоры:
Аналитическое выражение коэффициентов Aij для N-звенной модели биомеханической системы пост роим при условии введения в формулу динамических коэффициентов (Аij) символа Кронекера. Символ Кронекера равен
Здесь i, j - буквенные индексы, соответствующие цифровым индексам коэффициентов Aij. Используя символ Кронекера, можно записать представление коэффициентов Aij для N-звенной биомеханической системы в виде
Представление коэффициентов Aij в форме (2) делает быстрой и легкодоступной развернутую запись элементов матрицы Aij с любыми значениями индексов и позволяет автоматизировать процесс их формирования на ПК, задавая исходные данные по массивам: J, m, L, S. Назовем математическую модель, описываемую уравнениями (1), базовой математической моделью движения биомеханической системы. В зависимости от способа задания управляющих функций и моделирующего их алгоритма управления движением базовая математическая модель движения биомеханической системы трансформируется в подкласс конструктивных математических моделей синтеза целенаправленных движений человека. Результаты исследования. 1. Конструктивная математическая модель спортсмена на кинематическом уровне. Управляющие воздействия биомеханической системы формируются на двух уровнях: кинематическом (если управляющие функции заданы в форме пространственных либо пространственно временных характеристик) и динамическом (при задании управляющих функций в форме управляющих моментов мышечных сил). В соответствии с уровнем задания программного управления определяют два класса конструктивных математических моделей: с кинематическим уровнем задания программного управления и динамическим. Выделяя в классе конструктивных кинематических моделей в качестве управления изменение суставных углов спортсмена на всей траектории движения, уравнение (1) трансформируется в следующую математическую модель:
где p=2, 3, ..., N; ui =
Задав начальные условия движения модели (обобщенные координаты и обобщенные скорости звеньев модели) и используя программное управление (ui =
Так как программное управление является варьируемым параметром, то, изменяя его на всей траектории биосистемы, мы получим различные варианты техники моделируемого упражнения, из которых можно выбрать один, наилучший при определенных ограничениях, накладываемых на траекторию движения; кинематические, динамические ресурсы исполнителя, масс инерционные характеристики сегментов и звеньев тела. 2. Построение оптимальной техники соревновательных упражнений в вычислительном эксперименте. Движения человека как самоуправляемой системы можно описать системой дифференциальных уравнений, а следовательно, применить к ним методы математического аппарата. Используя методы оптимального управления динамическими системами, можно синтезировать наиболее эффективную технику спортивных упражнений. Один из методов поиска оптимального управления в теории оптимальных процессов, названный методом локальных вариаций, изложен в работе [3]. Его сущность заключается в том, что путем последовательных изменений программного управления в каждой точке дискретизации модели на шаг ±H изменяется траектория моделируемого процесса. Из всех возможных траекторий, определяемых шагом ±H, выбирается наилучшая в соответствии с заданным критерием качества исследуемого процесса. Далее шаг ±H делится пополам, и итерационный процесс продолжается до достижения сходимости функционала (когда критерий качества исследуемого процесса перестает изменяться на заданную величину точности). Если каждый элемент матрицы программного управления обозначить кружком, то ее структуру можно представить в виде схемы (рис. 2). Первоначально значения всех управлений, кроме первого, принимаются равными Um,j+(k); выполняется варьирование по элементам первого столбца матрицы при фиксированных значениях остальных значений управлений. Затем изменяется второе управление, принимая значение U2,j+(k-1), т. е. по второму столбцу матрицы варьирования опускаются на одну строчку. Значения управлений фиксируются, затем выполняется повторное варьирование для первого столбца. Такая последовательность перебора вариантов варьирования сохраняется до полного просмотра всех комбинаций управлений. Однако в результате вычислительных экспериментов выяснилось, что принятая схема вариаций в пространстве управлений не способна обеспечить выход из тупиковых ситуаций в точках локального минимума функций управления. Это связано с тем, что алгоритм метода исследует чрезвычайно узкое множество траекторий, ближайших к построенной траектории. В этом множестве может не оказаться лучшей, однако это не обязательно является свидетельством того, что уже построенное управление оптимально, поскольку алгоритм исследует не все возможные вариации. В этой связи мы разработали метод локально глобальных вариаций в пространстве управлений, который позволяет обеспечить наилучшее приближение к оптимальному управлению посредством дополнительных итерационных операций [2].
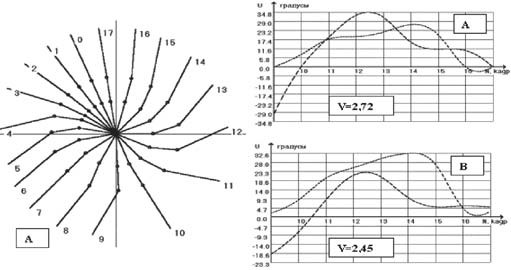
Рис. 2. Структура матрицы вариаций и схема перебора вариантов управлений при четырех управляющих воздействиях Скорость ОЦМ в момент прохождения гимнастом вертикали вверху в абсолютном значении (м/с) и в процентном отношении к идеальному исполнению для большого оборота назад на перекладине
3. Педагогический эксперимент. Цель педагогического эксперимента заключалась в обосновании эффективности обучения упражнениям на основе предварительных знаний занимающихся об идеальной индивидуальной технике изучаемых упражнений. Идеальная индивидуальная техника строилась по компьютерной программе с использованием разработанного авторами математического аппарата поиска оптимального управления. По направленности эксперимент был сравнительным, а по логической схеме доказательств - параллельным. Проводился он на базе СДЮШОР № 6 г. Могилева. В эксперименте приняли участие 16 гимнастов 13-14 лет. Методом случайного бесповторного отбора были сформированы экспериментальная (ЭГ) и контрольная (КГ) группы, по 8 человек в каждой. В качестве модельного упражнения был принят большой оборот назад на перекладине. Все испытуемые обучались по стандартной общепринятой методике. Различие заключалось в предварительном построении оптимальной техники исследуемых упражнений для испытуемых ЭГ. Модель оптимальной техники и кинетограмма упражнения служили для гимнастов ЭГ эталоном, к которому они должны стремиться. Для КГ такой эталон отсутствовал, и гимнасты ориентировались только на указания тренера и собственные представления об идеальной технике изучаемого упражнения. Эксперимент продолжался 3 месяца. В недельном цикле занятий испытуемые разучивали моделируемые упражнения два раза в неделю по семь подходов. До эксперимента никто из гимнастов обеих групп не исполнял больших оборотов на перекладине. За период эксперимента все испытуемые овладели техникой упражнения с различной степенью совершенства.
Рис. 3. Оптимальная траектория (А), оптимальное управление (А1) и управление после освоения большого оборота назад на перекладине (B) испытуемым с управлением в плечевых (- -) и тазобедренных (--) суставах по избранному критерию качества (V - линейная скорость ОЦМ тела спортсмена) В конце эксперимента перед всеми испытуемыми ставилась двигательная задача: с максимальной скоростью пройти вертикальное положение над опорой. Таким образом оценивался не просто уровень технического исполнения упражнений, а количественный показатель (скорость прохождения телом вертикального положения над опорой). На рис. 3 в качестве примера приведены предварительно построенные схемы оптимальной траектории и оптимального управления, а также реального управления после освоения изучаемого упражнения для одного из испытуемых. Результаты педагогического эксперимента свидетельствуют о том, что гимнасты ЭГ в среднем освоили большой оборот назад на перекладине на 85% относительно идеальной техники (имитационной математической модели движения) (см. таблицу). Средняя скорость ОЦМ спортсменов ЭГ после педагогического эксперимента составила 2,65 м/с, в то время как средняя скорость идеального исполнения - 3,11 м/с. Эти данные, а также достоверность различия по t-критерию Стьюдента между идеальной техникой и результатами, достигнутыми гимнастами ЭГ, показывают, что у последних существует резерв совершенствования технического мастерства. Средняя скорость ОЦМ спортсменов КГ составляет 2,09 м/с, т. е. 67 % относительно скорости ОЦМ при идеальной технике выполнения упражнения, и 79% относительно скорости ОЦМ спортсменов ЭГ. Различия между представителями КГ и ЭГ по скорости ОЦМ достоверны (р < 0,05). Заключение. Синтез движений на основе метода глобально локальных вариаций в пространстве управлений позволяет строить технику спортивных упражнений с заранее прогнозируемым изменением конфигурации биосистемы. Анализ результатов педагогического эксперимента показал, что предварительно построенная в вычислительном эксперименте оптимальная техника изучаемых упражнений способствует их эффективному освоению на более высоком техническом уровне и сокращению времени, затрачиваемого на процесс обучения. Литература 1. Донской Д. Д. Биомеханика: учеб. пособие для студентов факультетов физического воспитания пед. ин-тов / Д. Д. Донской. - М.: Просвещение, 1975. - 238 с. 2. Загревский В. И. Построение оптимальной техники спортивных упражнений в вычислительном эксперименте на ПЭВМ / В. И. Загревский, Д. А. Лавшук, О. И. Загревский. - Могилев: Могилев. гос. ун-т, 2000. - 190 с. 3. Моисеев Н. Н. Численные методы теории оптимальных управлений, использующие вариации в пространстве состояний / Н. Н. Моисеев // Кибернетика. - 1966. - № 3.
При любом использовании данного материала ссылка на журнал обязательна! | |||||||||||||||||||||||||||
 Доктор педагогических наук, профессор
В. И. Загревский
Доктор педагогических наук, профессор
В. И. Загревский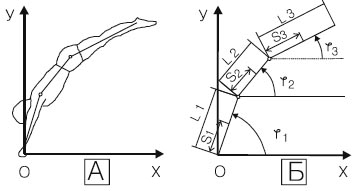
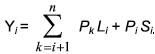
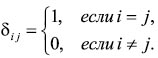
 (2)
(2) 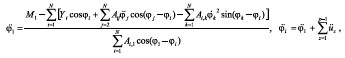 (3)
(3)