|
|

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ УЗЛА ПЕРЕМЕННОГО СОПРОТИВЛЕНИЯ МАШИНЫ БЕЗЫНЕРЦИОННОГО УПРАВЛЯЮЩЕГО ВОЗДЕЙСТВИЯ ДЛЯ АРМСПОРТА Кандидат педагогических наук, доцент В.Г. Свечкарёв,
Аспирант С.В. Поляков Кандидат педагогических наук, доцент
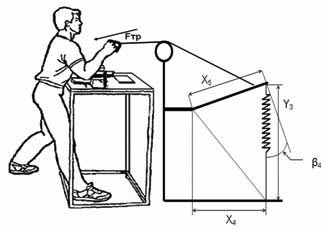
М.М. Эбзеев Ключевые слова: машины безынерционного управляющего воз действия, узел переменного сопротивления, математическая модель. Узел переменного сопротивления предназначен для использования в тренировочных устройствах, комплексах как нагрузочное устройство. Впервые в этом качестве он применен Ю.Т. Черкесовым, В.Г. Свечкаревым и А.С. Кожемовым (1996 г.) в тренировочном устройстве для развития силы мышц. Поскольку по методическим причинам необходимо начиная с некоторого уровня развития мышечной силы варьировать характер нагрузки, такой узел представляет практический интерес. Его полезно применять при тренировке дифференцированной мышечной силы, при занятиях армспортом и другими видами спорта, где важна не только силовая характеристика мышц, но и ловкость, точность движений и координация. Для конкретизации последующих рассуждений будем опираться на уже существующее устройство узел переменного сопротивления, примененный для тренировки армрестлеров. Этот узел в составе тренажера образу ют так называемую машину безынерционного управляющего воз действия (МБУВ), представленную на рис. 1.
Рис. 1. Машина безынерционного управляющего воздействия Тренажер представляет собой телескопическую стойку, за фиксированную на столе для армрестлинга. К стойке прикреплены два рычага: нижний, расположенный перпендикулярно стойке, посажен на втулку с фиксатором таким образом, что может перемещаться вверх или вниз по стойке, а верхний рычаг посажен на ось и может подниматься, переходя из горизонтального положения в вертикальное. На верхнем торце телескопической стойки закреп лен блок, который можно поднять или опустить, фиксируя телескопическую стойку на разной длине. Как нижний, так и верхний рычаги снабжены отверстиями для зацепления пружин и троса. К тросу, перекинутому через блок, придела на рукоятка, за которую спортсмен тянет на тренировке. Натяжение троса определяет силовую характеристику движения, которая может фиксироваться тензодатчиком, вставленным в разрыв троса. Исследуя графики силы реальных движений, выполненных на тренажере с таким узлом переменного сопротивления, Ю.Т. Черкесов, В.Г. Свечкарев и А.С. Кожемов показали, что на нем реализуются названные режимы сопротивления, и доказали их методическую ценность. Однако узел переменного сопротивления не изучался как таковой: не было сделано теоретического расчета проявляемой силы, её зависимости от положения рукоятки. Кроме того, кажется невероятным, что с помощью пружин (для которых справедлив закон Гука) можно реализовать постоянную величину силы натяжения троса на некотором участке перемещения рукоятки, а тем более убывание этой силы. Последующие рассуждения позволят доказать, что это так.
Рис. 2. Информационная модель
Рис. 3. Расчет момента упругого элемента Рассмотрим узел переменного сопротивления с упрощающими допущениями: все элементы конструкции будем считать невесомыми, все (кроме пружин) не растяжимыми, пренебрежем радиусом блока, силой трения и изменением коэффициента жесткости реальных пружин при их растяжении. При таких условиях систему можно считать квазистатической и применять к ней законы ста тики. Момент, создаваемый пружиной, можно найти как произведение силы на плечо: М = FX 2 cosβ3 = k(Y2 - Y20)X2 cos β3,где Y 20 - длина расслабленной пружины (рис. 2). Момент, создаваемый тросом:M = F тросаXlcоs β2.Значения cos β3 и cos β2 можно найти, исходя из теоремы косинусов:Угол в находим также из теоремы косинусов:
Решая приведенные уравнения в системе, с учетом того, чтомоменты сил со стороны пружины и троса уравновешиваются, получаем силу натяжения троса:
где Y1 рассчитывается так же, как записано ранее,
Рассмотрим математическую модель с параметрами, присущими реальному узлу переменного сопротивления: расстояние от блока до верхнего рычага C1=0,5 (м), расстояние от верхнего рычага до нижнего C2 =0,71 (м), расстояние от стойки до оси вращения С3 =0,045 (м). С помощью такого узла нетрудно реализовать режим возрастающего сопротивления. Для этого достаточно положить расстояние от оси вращения верхнего рычага до точки прикрепления троса X1=0,315 (м), от оси вращения верхнего рычага до верхней точки прикрепления пружины X2 =0,315 (м), от проекции оси вращения на нижний рычаг до точки прикрепления нижнего конца пружины X3=0,515 (м). Устройство имеет ограниченное число точек прикрепления пружин и троса (по девять на каждом рычаге). Убывающий режим сопротивления реализуется также достаточно просто: X1=0,315 (м), X2=0,315(м), X3=0,115(м). Постоянный (квазипостоянный) режим (на пятипроцентном уровне точности) реализуется с помощью двух групп пружин, расположенных в рассмотренных ранее двух положениях. Первая группа пружин, создающая возрастающий режим сопротивления, обладает коэффициентом жесткости в два раза большим, чем вторая. Для расчета нескольких групп пружин достаточно сложить значения силы для каждой из их групп. Величину натяжения троса можно менять с помощью изменения расстояния C2, количества пружин и, если не нужно точно придерживаться режима сопротивления, то и изменением положения точек прикрепления пружин и троса. Для создания убывающе-возрастающего режима сопротивления необходимо добавить еще один упругий элемент, который конструктивно представляет собой пружину, один конец которой соединен с верхним рычагом, а другой - с тросом, длина которого может регулироваться в зависимости от потребности во включении упругого элемента в нагрузку в нужной фазе движения (см. рис.1). Для расчета момента, создаваемого этим элементом, нужно ввести координаты прикрепления верхнего (Х5) и нижнего (Х4) конца и начальную длину всего упругого элемента (Y3n) и его собственно упругой части (Y30) (рис.3), тогда: Mпт = FптX5cоs β4, где
k - коэффициент жесткости пружины, β4 - νаходится из теоремы косинусов: (С22 + Х42 = X52 + Y32 - 2Х5 Y3 cos(90° - β4)). Сумму моментов, создаваемых группой упругих элементов и тросом с рукояткой, можно приравнять к нулю, следуя ранее введенным упрощающим допущениям. Для создания выраженного убывающе-возрастающего режима сопротивления пружина для упругого элемента должна быть в 2 раза жестче. Крепится пружина, как показано на рис. 1. Используя приведенные выше параметры, можно построить графики зависимости величины силы от положения рукоятки. На графиках (рис. 4) отображены виды функций для различных режимов сопротивления. Необходимо отметить, что ни один из этих режимов нельзя реализовать с помощью системы грузов и блоков, так как грузы обладают инерционностью, которая искажает режим сопротивления при наличии ускорения движения рукоятки. Таким образом, можно считать достигнутой цель исследования: найдены пути решения задачи, показаны четыре основных режима сопротивления. Этот результат имеет важное практическое значение, так как позволит легко ориентироваться в подборе режимов сопротивления и заранее предсказать, какой режим сопротивления реализуется при каком-либо положении пружин.
Рис. 4. Режимы сопротивления
При любом использовании данного материала ссылка на журнал обязательна! |



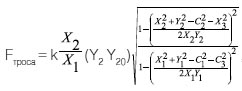 ,
,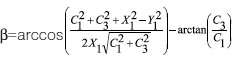
 - сила натяжения упругого элемента (пружины с тросом),
- сила натяжения упругого элемента (пружины с тросом), 