О ВОЗНИКНОВЕНИИ И КООРДИНАЦИИ РИТМИЧЕСКИХ ДВИЖЕНИЙ

МЕТОДОЛОГИЯ БИОМЕХАНИ-
ЧЕСКОГО ИССЛЕДОВАНИЯ

Abstract

ABOUT BEGINNING AND COORDINATION OF RHYTHMIC MOVEMENTS

A.V. Kurgansky, doctor of biology

Moscow state university

Key words: rhythmic movements, functional system, structure, circular scheme of control, central timer, motor programme, coordination of bemanual movements.

The purpose of this paper was to discuss the outcomes that follow from the circular principle realizing in movements' control concerning presented with rhythmic movements emergency theoretical modelling.

As a result of our theoretical research it had become possible to show that the spontaneous change in coordination of bemanual movements can be watched without any external sensory signal that drives the rate of movements. Our model posesses the essential features of the real coordination dynamics - the primary use of the antiphase and inphase coordination modes and the spontaneous transition between them.

We hope that the study of the quantative characteristics in rhythmic movements can open the new opportunities to penetrate into the structural organization of functional systems.

О ВОЗНИКНОВЕНИИ И КООРДИНАЦИИ РИТМИЧЕСКИХ ДВИЖЕНИЙ¹

Кандидат биологических наук А. В. Курганский Московский государственный университет им. М.В. Ломоносова

Ключевые слова: ритмические движения, функциональная система, структура, кольцевая схема управления, центральный таймер, моторная программа, координация бимануальных движений.

Положение Н.А.Бернштейна (1947, 1966) о том, что стоящая за движением функциональная система строится по принципу кольца, составляет основу большинства современных теоретических представлений об управлении произвольными движениями (см.: Гордеева, 1995; Шапков и др. 1988, Rosenbaum, 1994).

К сожалению, при построении теоретических моделей ритмических движений этот фундаментальный принцип долгое время недооценивался.

Внешняя простота ритмических движений, их высокая упорядоченность в пространстве и во времени как бы провоцировали исследователей на поиск столь же простых внутренних механизмов ритмогенеза. Многие исследователи рассматривали вопрос о формировании ритмических движений как часть более общей проблемы серийной организации движений. При этом полагали, что изолированные двигательные фрагменты объединяются в серии под управлением некоего внутреннего объединяющего начала - моторной программы (Rosenbaum, 1994). Основные усилия представителей этого направления были сосредоточены на поиске внутренней структуры моторной программы, непременным атрибутом которой оказывался таймерный механизм (или, как чаще говорят в отечественной литературе, - временная развертка), который в одних случаях рассматривался как часть самой моторной программы (Rosenbaum, et al., 1983), а в других - как надмодальный, не связанный с моторной системой центральный таймер (Vorberg, Hambuch, 1984; Wing, Kristofferson, 1973).

С точки зрения теории самоорганизации -относительно нового научного направления, -ритмические движения не являются результатом объединения отдельных движений в серии или циклы, и поэтому не требуется ни координирующего механизма или программы, ни специального таймера, отвечающего за ритмическую организацию (Kelso, 1995; Turvey, 1990).

Теория самоорганизации считает источником возникновения ритмических движений спонтанные флуктуации (случайные колебания сигнала), неизбежно присутствующие в любой сложной открытой системе (Пригожин, 1985; Пригожий, Стенгерс, 1994; Kelso, 1995), каковой и является двигательная система. При определенных условиях в ней возникает усиление некоторых частотных составляющих флуктуации, которые начинают доминировать в коллективном поведении всей сложной системы.

В результате все участники взаимодействия (нейронные сети ЦНС, мионевральный аппарат и кинематическая система конечности) вовлекаются в общий процесс упорядоченных колебаний, т.е. возникает макроскопически упорядоченное коллективное состояние всей системы. Происходит динамическое связывание избыточных степеней свободы двигательной системы человека посредством общего сигнала, принимающего в пределах ЦНС форму нейронной активности, а вне ее -форму механических движений и порождаемых ими сенсорных сигналов. Принцип динамического связывания избыточных степеней свободы двигательной системы является обобщением (Kelso, 1995) предложенного Н.А. Бернштейном принципа сенсорных коррекций как способа преодоления кинематической избыточности опорно-двигательного аппарата, превращения его в управляемую систему.

Однако теория самоорганизации ритмических движений, по крайней мере в ее современном виде, недооценивает роль структуры функциональных систем управления движениями, исходя из того, что эта структура несущественна для самого факта возникновения ритмического "коллективного состояния" (Haken, Kelso, Bun2,1985; Kelso, 1995). С такой позицией нелегко согласиться, если принять во внимание многочисленные клинические и нейропсихологические данные, говорящие об отчетливой специфической зависимости пространственно-временных параметров ритмических движений от характера, локализации и степени поражения мозга. Неправомерность игнорирования структуры делается совершенно очевидной, если попытаться применить теорию самоорганизации ритмических движений к случаю локального поражения представительства руки в первичной моторной зоне коры. Действительно, выпадение функции этой области ведет к полной неспособности выполнять пораженной рукой какие бы то ни было произвольные движения. .

Между тем, локальное поражение коры не означает прекращения сложного нелинейного взаимодействия на субкортикальном уровне. Все условия возникновения упорядоченных состояний сохраняются, и остается совершенно непонятным, почему же возникновение ритмических движений оказывается невозможным в парализованной руке.

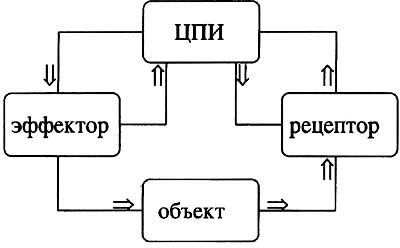
Рис. 1. Упрощенная схема кольцевой функциональной системы управления движениями

По-видимому, и сам факт возникновения ритмических движений, и их характер самым тесным образом связаны со структурой функциональной системы. В этой работе мы покажем, что ритмические движения могут быть обязаны своим происхождением именно кольцевому характеру управления и что кольцевая схема управления может одновременно выступать и как таймер, и как программа, определяющая характер возникающего в ней ритма.

Возникновение ритмических движений в кольцевой схеме управления.

На рис.1 представлена упрощенная схема кольцевого управления движениями. Мы намеренно упростили эту схему, оставив в ней только четыре блока, которые для краткости обозначили как "эффектор", "объект", "рецептор" и "центральный блок преобразования информации" (ЦПИ), поскольку большая детализация несущественна для дальнейшего обсуждения.

Носителем информации в кольцевой системе является сигнал, который непрерывно преобразуется из одной формы в другую: эффектор преобразует его из нейронной импульсации в механическое движение управляемой конечности; в свою очередь, механическое движение конечности и ее взаимодействие с внешним объектом вызывают появление различного рода рецепторных сигналов (потенциалов мышечных, сухожильных, тактильных, дистальных рецепторов); наконец в рецепторе сигнал вновь приобретает вид нейронной имульса-ции. Непрерывная циркуляция сигнала в кольцевой схеме управления приводит к тому, что на вход каждого блока этой схемы поступает сигнал этого же блока, прошедший все другие блоки кольца и подвергшийся в них преобразованиям. Для определенности будем говорить о сигнале эффектора (т.е. о наблюдаемом положении конечности) и обозначим это положение символом x(t). Важно учесть два существенных обстоятельства. Во-первых, все компоненты кольцевой схемы являются источниками принципиально неустранимых вариаций сигнала - спонтанных флуктуации. Во-вторых, сигнал не может "обежать" кольцо мгновенно, для этого ему потребуется определенное время. Все это можно выразить очень коротко, воспользовавшись математическим понятием оператора (абстрактного правила преобразования):

(1) x(t) = B[x(t-d)] + e(t),

где символом d обозначена суммарная временная задержка, набегающая при прохождении сигнала x(t) вдоль всего кольца, e(t) соответствует флуктуациям, а оператор В[ ] заключает в себе все те преобразования (быть может, очень сложные и пока неизвестные), которым подвергается сигнал, проходя вдоль цепочки"эффектор-объект-рецептор-ЦПИ-эффектор", прежде чем вернется обратно в блок "эффектор" через время d.

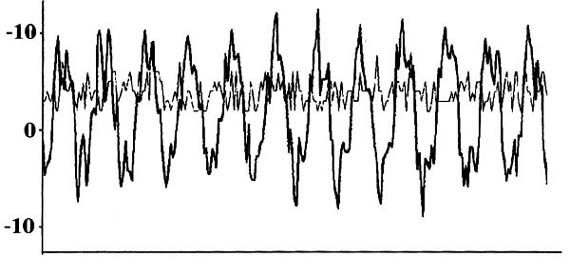
Рис. 2. Ритмические колебания, возникающие из шума в кольцевой системе управления движениями. Результаты численного моделирования выражения (2). Толстая линия - x(t); тонкая линия - e(t)

Возможны две точки зрения на причину возникновения ритмического сигнала и, следовательно, движений в кольцевой схеме управления. Одна из них, которую мы назовем "информационной", исходит из того, что для возникновения ритмических движений требуется соответствующая информация о временных и пространственных характеристиках этих движений. При этом предполагается, что необходимую информацию содержит блок ЦПИ и что именно этот блок - источник сигнала. Таким образом, ритмическое движение возникает в результате работы некой эндогенной программы и роль кольца в этом случае хотя и существенна, но пассивна: эфферентная часть кольца доставляет управляющую информацию к эффектору, предварительно преобразовав ее в форму центральных команд, а афферентная часть позволяет осуществлять сенсорные коррекции. Естественно, что с "информационной" точки зрения и спонтанные флуктуации сигнала, несущего полезную информацию, и задержка, связанная с проведением сигнала, рассматриваются как негативные свойства, как следствие несовершенства биологических систем.

Однако возможен и иной взгляд, тесно связанный с теорией самоорганизации, согласно которому оба этих "негативных" фактора, наоборот, играют конструктивную роль. Обратим внимание на то, что операторное уравнение (1) описывает не только правила преобразования информации от блока к блоку, но и временную эволюцию сигнала, являющегося носителем этой информации. Фактически, как мы видели, "информационная" точка зрения предполагает, что без активного источника сигнала, скрытого в операторе В[ ], ничего, кроме незначительных флуктуации e(t), в кольцевой схеме управления происходить не будет. Однако это неверно. Даже при неизменном во времени характере преобразований (т.е. при не зависящем от времени операторе В[ ] в кольцевой схеме могут и будут самопроизвольно возникать сигналы, характер которых не противоречит уравнению (1). В приложении А показано, что если действие оператора В[ ] сводится к любой функциональной зависимости x(t) от x(t - d), то в кольцевой схеме управления обязательно будет возникать и распространяться именно ритмический сигнал, временная эволюция которого описывается функциональным уравнением: (2) x(t) = m x(t - d) + e(t).

Другими словами, в этом случае кольцевая схема управления должна вести себя как усилитель с коэффициентом усиления m и задержанной на время d обратной связью.

Характер сигнала, описываемого уравнением (2) и полученного в результате численного моделирования этого уравнения, показан на рис. 2. В качестве e(t) моделирования был выбран случайный сигнал, типичный для спонтанной импульса-ции нейронов ЦНС (Жадин, 1984).

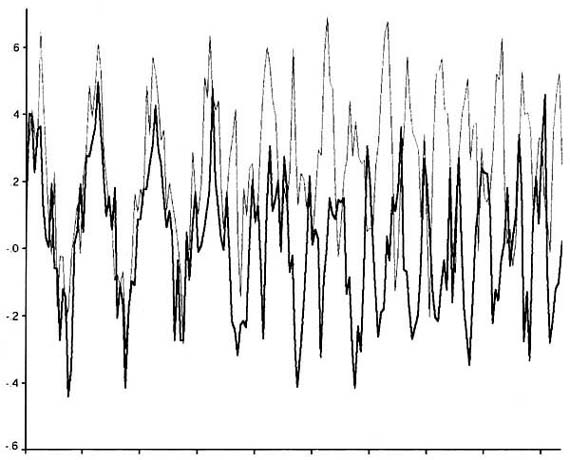
Рис. 3. Спонтанный переход реципрокных движений в синхронные в численном эксперименте. Толстая линия - x(t); тонкая линия - e(t). Пояснения в тексте

В соответствии с изложенной точкой зрения, альтернативной "информационному" подходу, ритмический сигнал формируется всей кольцевой системой в целом, и, следовательно, эта система играет роль и "центрального таймера", и "моторной программы" одновременно. Спонтанные флуктуации сигнала служат тем энергетическим и информационным "материалом", из которого зарождается ритмический сигнал. Шум выступает здесь в своей созидательной роли, являясь как бы резервуаром возможного, источником необходимой функциональной избыточности (Бернштейн, 1966; Kelso, 1995). Как мы убедились, кольцевой характер функциональной системы и тот факт, что сигналу требуется конечное время d для того, чтобы полностью обежать кольцо, ответственны за ритмический характер возникающего из шума сигнала. Таким образом, если шум является источником возможных движений, то характер преобразований в кольцевой схеме управления служит принципом отбора актуального.

Оттого, какие именно преобразования информации "скрыты" за оператором В[ ], зависят та или иная форма и амплитуда ритмического движения. Следовательно, изменение характера ритмических движений может быть достигнуто за счет изменений оператора В[ ], например, за счет включения (или исключения) в функциональную систему управления движениями каких-то новых функциональных блоков. Таким образом, кодируется или программируется (и соответственно, хранится в долговременной памяти и извлекается из нее) не репрезентация ритмических движений как таковых, а структура той функциональной системы, естественным свойством которой является порождение ритмических движений требуемого вица.

О координации бимануальных ритмических движений.

Применим изложенные выше представления к проблеме возникновения и координации ритмических бимануальных движений. Упрощая ситуацию, примем, что бимануальные ритмические движения формируются и координируются функциональной системой, куда симметрично входят моторные отделы левого и правого полушарий, оказывающие друг на друга равное по силе тормозящее воздействие.

Рис.4. Спонтанный переход реципрокных движений в синхронные и обратно при выполнении реципрокного теппинга ребенком 6 лет.
По горизонтальной оси - время в с. Пояснения в тексте

Нетрудно убедиться (см. приложение Б), что организованная таким образом функциональная система породит координированные ритмические движения, причем устойчивыми окажутся только два режима координации - синхронный (руки движутся с нулевым сдвигом по фазе) и реципрок-ный (руки движутся с фазовым сдвигом в 180°) Кроме того, флуктуации сигнала приведут к тому, что организованная таким образом функциональная система будет демонстрировать спонтанные переходы от одного координационного режима к другому. Эти выводы подтверждаются и результатом численного эксперимента - моделированием динамики сигналов r(t) и 1(t), описываемой уравнениями (Б.1) и (Б.2). Пример спонтанного перехода от реципрокной координации к синхронной, наблюдаемого в численной модели, - на рис.3.

Явление спонтанного перехода от реципрокной к синхронной координации рук впервые было обнаружено экспериментально (испытуемых просили синхронизировать движения рук с ударами метронома, темп которых медленно увеличивался) и фактически послужило исходным пунктом построения синергетической теории биману-альных координации (Haken, Kelso, Bunz, 1985; Kelso, 1995). Однако самопроизвольную смену способа координации рук можно наблюдать, как и предсказывает наша модель, без внешнего, задающего темп движений сенсорного сигнала. Пример такого перехода приведен на рис. 4, где показаны движения ребенка б лет, которого просили выполнять альтернативный теппинг в максимальном темпе. Отчетливо видно, что ребенок, начав выполнять в соответствии с инструкцией реципрокные движения, на 3-й с спонтанно перешел к выполнению синхронных движений, а на 9-й с вновь вернулся к требуемому реципрок-ному режиму координации.

Таким образом, даже столь простая модель, которую мы только что рассмотрели, обладает существенными чертами реальной координационной динамики - преимущественным использованием реципрокного и синфазного способов координации и явлением спонтанного перехода между ними.

Экспоненциальное уменьшение мощности нейронного шума на высоких частотах (Жадин, 1984) позволяет объяснить обычно наблюдаемое (Kelso, 1995) уменьшение амплитуды ритмических движений по мере возрастания их частоты -ритмический сигнал рекрутируется из частотных составляющих шума, мощность которых систематически убывает по мере возрастания их частоты.

Заключение. Подчеркнем, что рассмотренный нами процесс зарождения ритмических движений в функциональной системе, организованной по типу "рефлекторного кольца", не является очередным алгоритмом, специально сконструированным для порождения ритмических движений. Наоборот, ритмические движения могут спонтанно возникать в любых "закольцованных" системах при достаточно широком классе функциональных преобразований сигнала.

Наш подход в отличие от синергетических теоретических моделей (Haken, Kelso, Bunz, 1985) не просто исходит из наличия ритмов как из данности, а связывает их происхождение со структурой функциональной системы (в данном случае с ее кольцевым характером) и в этом смысле объясняет генез ритмических движений.

Можно надеяться, что изучение количественных характеристик ритмических движений откроет новые возможности для проникновения в структурную организацию функциональных систем.

Автор выражает благодарность В.П.Зинченко, Н.Д.Гордеевой, Т.В.Ахутиной и А.Н.Кричевцу за ценные замечания и доброжелательную критику первоначального варианта статьи.

ПРИЛОЖЕНИЕ А

Пусть преобразования сигнала в кольцевой схеме управления, описываемые операторным уравнением (1), соответствуют некоторой (быть может, очень сложной) функции В[ ]. Прежде всего должно найтись такое значение x₀, при котором x₀ = В[x₀]. Этому постоянному значению сигнала соответствуют неизменное положение конечности в пространстве и определенное тоническое состояние. Если изменится оператор В[ ], то изменится и положение покоя x₀ - конечность займет новое положение в пространстве. Поскольку источник энергии флуктуирует, то даже в покое будут наблюдаться и флуктуации положения конечности - тремор покоя.

Пусть Xo является одной из устойчивых точек равновесия кольца, т.е. одним из решений уравнения x₀ = B[x₀]. Представим сигнал x(t) в виде суммы постоянного значения x₀ и достаточно малых отклонений y(t) от него: (А.1) x(t) = x₀ + y(t). Тогда исходное уравнение (1) можно записать в виде (А.2) x₀ + y(t) = В[x₀] + y(t - d)] + e(t) или после линеаризации (A.3) x₀ + y(t) = B[x₀] + В'у[x₀] y(t - d) + e(t). Сокращая x₀ в левой части уравнения и В[x₀] в правой, окончательно получим: (А.4) y(t) = m y(t - d) + e(t), где множитель m равен B'y[x₀], т.е. значению производной функции В[х] в точке x₀.

Характер всех совместных с уравнением функций y(t) проще всего выяснить, перейдя к частотному представлению с помощью интегрального преобразования Фурье (Колмогоров, Фомин, 1976), что является математически корректным при условии ¦m¦ < 1, которое, кстати, совпадает с условием устойчивости точки Хo и справедливости применения линейного приближения (А.4). В результате такого перехода получим: (А.5) Y() = m ехр(i d) Y() + Е(), откуда получается выражение для спектральной плотности мощности (СПМ) сигнала y(t): (A.6) S_y() = S_e(w) / [1 - 2m cos(d) + m²], где - частота, S_e() - СПМ шума, a S_y() - СПМ сигнала.

Соотношение (A.6) показывает, что спектр сигнала S_y() формируется за счет избирательного усиления тех частотных составляющих шума S_e(), для которых величина знаменателя будет меньше единицы. Например, при m > 0 знаменатель будет минимальным при условии cos(d) = 1, которому соответствует гармонический ряд частот _k = 2 k/d (k = 0, 1, 2, ...).

Составляющие сигнала с частотами wk будут усилены в 1 / (1-m)2 раз, что может оказаться достаточно большой величиной, если m мало отличается от единицы. Это как раз и означает, что сигнал y(t) представляет собой квазипериодическое колебание с периодом d.

Причина избирательного усиления множества равноотстоящих друг от друга частотных составляющих шума e(t) заключается в запаздывании d, благодаря которому в (А.6) присутствует периодически изменяющаяся с частотой величина 2mcos (d). Действительно, если в (А.6) положить d = 0 (это соответствовало бы бесконечной скорости распространения сигнала), то получим cos(d) = 1 и, следовательно, S_x() = S_e() / (1 - m)², что (при m > 0) соответствует простому равномерному усилению мощности шума в (1 - m)² раз во всем частотном диапазоне.

ПРИЛОЖЕНИЕ Б

Пусть 1(t) и r(t) обозначают сигналы, управляющие движением, соответственно, правой и левой рук, а величины e_r(t) и e_l(t) соответствуют флуктуациям этих сигналов. Взаимное торможение описывается системой уравнений, подобных уравнению (2):

(B.l) r(t)+ml(t-d)=e_r(t)

(Б.2) 1(t) + mr(t - d) = e_l(t).

Здесь коэффициент m < 0 характеризует степень взаимного подавления левой и правой моторных систем, а d соответствует временному запаздыванию, с которым такое влияние происходит.

Переходя в частотную область, нетрудно убедиться, что такая система будет усиливать частотные составляющие шума, принадлежащие дискретному ряду _k=/2d, (k = 0, 1, 2, ...), в соответствии с формулами:

(Б.З) R(_k) = [Еr(_k)± Еr(_k)] / (1 - m2)

(Б.4) L(_k) = [Е_l(wk) ± E_r(_k)]/(1 - m2), где R(_k) и L(_k) означают Фурье-изображения сигналов r(t) и 1(t), а Е_r(_k) и Е_l(_k) - Фурье-изображения e_r(t) и e_l(t). При этом знак "-" соответствует нечетным, знак "+" - четным значениям индекса k.

При нечетных значениях индекса k получим R(_k) = -L(_k), т.е. колебания происходят в противофазе, в то время как при четных k имеем Р(_k) = L(_k), т.е. колебания оказываются синфазными.

Литература

1. Бернштейн Н.А. О построении движений. M., 1947.

2. Бернштейн Н.А. Очерки по физиологии движений и физиологии активности. M., 1966.

3. Гордеева Н.Д. Экспериментальная психология исполнительного действия. M., 1995.

4. Жадин M.H. Биофизические механизмы формирования электроэнцефалограммы. M., 1984.

5. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. M., 1976.

6. Пригожий И. От существующего к возникающему. M., 1985.

7. Пригожий И., Стенгерс И. Время, Хаос, Квант. M., 1994.

8. Шапков Ю.Т., Анисимова Н.П., Герасименко Ю.П., Романов С.П. Регуляция следящих движений. Л., 1988.

9. Haken H., Kelso J.A.S., Bunz H.A. Theoretical Model of Phase Transitions m Human Hand Movements //Biol. Cybern. 1985. Vol. 51.

10. Kelso J.A.S. Dynamic Patterns. The self-organization of brain and behavior. Cambridge, MA, London, England, 1995.

11. Rosenbaum D.A., Kenny S., Derr M.A. Hierarchical control of rapid movement sequences //J. of Exper. Psychol.: Human perception and performance. 1983. Vol. 9.