КОНСУЛЬТАЦИИ

Smimov M.R.

Key words: running loading, repeated loadings' method, number of stretches reiterations, method of "limiting curves", metabolic source, bioenergetic spectrum.

В ПОМОЩЬ ТРЕНЕРУ

НАУЧНО ОБОСНОВАННОЕ ЧИСЛО ПОВТОРЕНИИ ОТРЕЗКОВ БЕГОВОЙ НАГРУЗКИ

Доктор педагогических наук М.Р. Смирнов
Новосибирский государственный педагогический университет

Ключевые слова: беговая нагрузка, повторная тренировка, число повторений отрезков, метод "предельных кривых", метаболический источник, биоэнергетический спектр.

Введение. Появление повторного метода в беговой нагрузке официально относится к 20-м годам уходящего столетия, когда финские специалисты, работавшие с бегунами на выносливость, с успехом апробировали этот методический подход, воспитав целую плеяду выдающихся стайеров во главе с легендарным Пааво Нурми.

Хотя слабо верится в то, что американские спринтеры, выигрывавшие первые олимпиады современности на рубеже двух столетий, не использовали повторных пробеганий спринтерских отрезков в своих тренировках.

Мало того, даже древние греки, бегавшие свой "стадий", вряд ли ограничивались однократным пробеганием при подготовке к соревнованиям.

Но так или иначе, следует констатировать, что повторный метод беговой нагрузки прочно вошел в технологию спортивной подготовки и со временем получил должное обоснование в исследованиях биохимиков и физиологов.

Однако обоснование получил сам подход, а что касается максимального количества повторений конкретного отрезка в одном тренировочном занятии, то нужно признать, что к настоящему времени спортивная наука располагает лишь отрывочными рекомендациями, разбросанными по крупицам в работах по исследованию биохимии мышечной деятельности, а также весьма разноречивыми сведениями из спортивной педагогики.

В результате в течение примерно двух третей XX столетия усилиями специалистов-практиков шло неуклонное наращивание числа повторений и данный тренировочный параметр был доведен до весьма внушительных размеров (например, 100х400 м у марафонцев или 120х30 м у спринтеров).

В течение последней трети XX века начался обратный процесс, который может быть проиллюстрирован следующей цитатой из "Учебника тренера по легкой атлетике": "... в последние годы наблюдается определенная тенденция к уменьшению количества пробегаемых отрезков. Если Э. Затопек, В. Куц, И. Филин, Р. Мунс и другие выполняли от 20 до 100 повторений на отрезках, 100-400 м, то в настоящее время на этих же дистанциях, в тренировке, ведущие бегуны мира в одном занятии не делают более 20-40 повторений" [9, с. 173].

Уже после выхода в свет этого учебника, в середине 80-х гг., было известно, что ведущие спринтеры ГДР применяли разовую дозировку, не превышавшую. 15х300 м.

Таким образом, можно констатировать, что, несмотря на уменьшение объема разовой нагрузки, продолжался неуклонный рост спортивных результатов. Сопоставление двух процессов наводило на мысль, что используемые практиками величины такого параметра, как число повторений, далеки от оптимальных.

Возражения отдельных специалистов по поводу того, что отрезок 300 м в тренировке стайеров и спринтеров - совсем не одно и то же и что Э. Затопек 100х400 м бегал чуть ли не шагом, лишь укрепляли уверенность в том, что такой параметр, как число повторений, должен быть "привязан" не к длине отрезка, а к метаболическому режиму, на который в данном случае оказывается тренирующее воздействие. То есть получалось, что точное решение, казалось бы, чисто педагогической задачи становилось возможным лишь при использовании закономерностей биоэнергетики.

Биоэнергетическое обоснование. В наших предыдущих исследованиях [3-8] беговая нагрузка увязывалась с метрическими и временными параметрами полного биоэнергетического спектра, состоящего из ряда основных и промежуточных (переходных) метаболических источников, каждый из которых был представлен мощностной и емкостной составляющими.

Исходя из таких предпосылок, следует отметить, что прежде всего максимальное число повторений конкретного отрезка должно гарантировать соответствующую проработку мощностной или емкостной составляющей определенного метаболического источника [8].

Кроме того, количество повторений должно быть увязано с методологической концепцией тренирующего воздействия на конкретный метаболический источник, сводящийся к преодолению тренировочных отрезков в пределах данного диапазона со скоростью, варьируемой в рамках скоростного диапазона [3].

И, наконец, дозировка числа повторений (как, впрочем, и любого параметра спортивной нагрузки) должна зависеть от спортивно-квалификационного уровня, специализации и пола занимающихся.

Учитывая изложенные условия, можно констатировать, что число повторений является функционалом как минимум шести переменных: 1) метаболического режима (R_m) 2) длины отрезка в пределах данного режима (I), 3) скорости пробегания (V), 4)' квалификационного разряда (R_k) 5) специализации (Sp) и 6) пола спортсменов (Sx), то есть i_t = F (R_m,l,V,R_k,Sp,Sx). (1)

Получению точного математического решения препятствуют два обстоятельства: во-первых, отсутствие необходимого количества исходных биоэнергетических данных и, во-вторых, необходимость выбора не слишком сложного алгоритма, который был бы понятен специалистам спортивной педагогики;

ведь в конечном итоге результатами расчета предстоит пользоваться именно им.

Поэтому предлагается приближенный, во многом упрощенный вариант. Однако уже то обстоятельство, что при данном подходе используется полный биоэнергетический спектр, позволяющий охватить всю легкую атлетику в целом (со всеми специализациями и разрядными уровнями), дает возможность получить уточненные, а самое главное обоснованные величины числа повторений (i_t) для бесконечного множества тренировочных вариантов.

Исходя из существующих эмпирических положений, можно констатировать, что в отношении сверхдлинных дистанций возможно лишь одно повторение в процессе тренировочной работы, в то время как при построении тренировочных программ для спринта используются десятки повторений коротких отрезков.

Вместе с тем можно отметить, что с изменением длины дистанции изменяется и мощность метаболического источника, превалирующего в энергообеспечении; при этом, как явствует из полного биоэнергетического спектра, мощность источников, отвечающих за энергоснабжение спринтерских дистанций, много выше, чем мощность "стайерских" источников.

Из этого можно сделать вывод, что при технологической проработке метаболических источников большей мощности потребуется и большее число повторений.

То есть получается, что число повторений (i_t) прямо пропорционально мощности превалирующего метаболического источника (N). Но поскольку мощность в зависимости от длины отрезка изменяется по гиперболе (являющейся частным случаем степенной функции) [5], то и число повторений должно также изменяться по гиперболе, но со своими показателями.

Следовательно, в общем виде можно записать, что i_t=aI^-b. (2)

В логарифмических координатах это будет прямая линия вида Y = А-bХ, где Y = lgit, A = lga и Х = lgI.

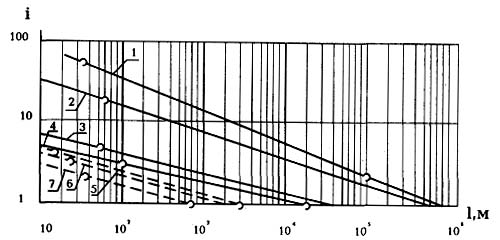
Шкала МСМК

8 16 32 64 128 256 512 1024 2048 4096 8192

Шкала детей 10 лет

6,5 13 26 52 104 208 416 832 1664 3328

Рис. 1. Графическая интерпретация метода "предельных кривых": I - максимальное число повторений бегового отрезка;

I - метрические параметры метаболических режимов беговой нагрузки; 1 - I_tmax для мужчин-мсмк; 2 - I_tсрд для мужчин-мсмк; 3 - I_tmin, для мужчин-мсмк; 4 - Iсрв для мужчин-мсмк; 5 - I_tmax. для мальчиков 10 лет; 6 - I_tсрд для мальчиков 10 лет; 7 - I_tmin для мальчиков 10 лет

Если бы все отрезки преодолевались с одной и той же, скажем, соревновательной интенсивностью, то можно было бы ограничиться одной такой кривой. Но поскольку реальный тренировочный процесс предполагает множество вариантов интенсивности, то начинать нужно с нахождения пределов этого множества.

Если обратиться к методологической концепции тренирующего воздействия на метаболический источник [3], то можно обнаружить пять принципиальных рубежей. Во-первых, соревновательный вариант с интенсивностью ti (Ii) или Ii (Ii) (т.е. когда отрезок Ii преодолевается в соревновательном темпе Ii). При этом по каждому метаболическому источнику будет возможно лишь какое-то минимальное число повторений - icpв. Во-вторых, наиболее жесткий тренировочный вариант с интенсивностью ti(ti') или Ii(Ii'), которому соответствует i_tmin. Далее существуют два средних рубежа - t_i-1(t_i') (или I_i-1(I_i')) и t_i(t_i+1) (или I_i(I_i+1)) с числом повторений itсрд. И, наконец, наименее интенсивный тренировочный вариант t_i-1(t_i+1) (или I_i-1(I_i+1)) с числом повторений - i_tmax.

Метод "предельных кривых". При разработке алгоритма был применен метод, которому можно дать название "метод предельных кривых". В данном случае кривые оказались гиперболами, но при расчете других параметров беговой нагрузки, где также применялся этот метод, аналогичные кривые были представлены другими функциями; поэтому в общем виде следует остановиться на вышеупомянутом термине.

Расчет алгоритма был произведен на примере мужской части легкой атлетики; то есть тем самым уже учитывается один из вышеперечисленных аргументов (см. уравнение 1).

Как отмечалось в предыдущем изложении, основные уровни интенсивности, соответствующие методологической концепции тренирующего воздействия, могут быть представлены зависимостью (2). Каждая такая кривая, согласно уравнению 2, проходит через весь биоэнергетический спектр, т.е. является общей для всех метаболических источников. Подобные кривые, вычисленные для предельных контингентов - мужчин-мсмк и мальчиков 10 лет, нанесены на логарифмический график (рис. 1).

Можно заметить, что кривые, изображенные на этом графике, являются предельными в трех измерениях. Во-первых, каждая из них ограничивает число повторений при беговой нагрузке определенной интенсивности; во-вторых, кривые, соответствующие itmax и itmin являются пределами для всех максимальных значений it используемых при тренировке бегунов данного спортивного квалификационного уровня; и, наконец, в-третьих, представленные на графике спортивные контингенты являются предельными для рассматриваемого периода спортивного онтогенеза (все остальные разрядные уровни располагаются между кривыми для мсмк и новичков). Все перечисленные обстоятельства явились основанием для наименования метода, использованного при решении данной проблемы.

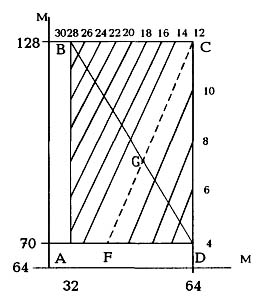
Рис. 2. Номограмма для определения максимального числа повторений тренировочных отрезков беговой нагрузки при проработке метаболического режима Е₃ у мужчин-мсмк

Поскольку в логарифмических координатах каждой из рассматриваемых кривых соответствует прямая линия (см. рис. 1), то для построения такой прямой достаточно двух точек;

однако их координаты по возможности не должны вызывать сомнений. Причем для большей точности эти точки должны быть максимально удалены друг от друга, т.е. искать их следует в спринтерских и стайерских режимах.

Начнем с объяснения зависимости iсрв = f(I) (кривая 4 на рис. 1). В соревнованиях спортсменов высокого ранга встречаются варианты/коммерческих и прочих стартов, проводимых в один день. Причем в программе присутствуют все спринтерские дистанции. На таких соревнованиях спортсмены иногда выступают в забеге и финале бега на 100 м, а также в беге на 200 м. Даже если учесть, что финалисты бега на 100 м пробегают свой предварительный забег вполсилы, то и в этом случае для такого отрезка, как 100 м можно гарантированно принять iсрв = 3.

Для нахождения второй точки следует определить дистанцию, максимально отвечающую параметру icpв = 1. Формального соблюдения одного такого условия недостаточно, так как любую дистанцию, вплоть до самых длинных, можно пробежать в соревновательном темпе один раз.

Следовательно, требуется дополнительное ограничение. В качестве такого ограничения может быть принято отсутствие дополнительного питания на дистанции. Дело в том, что весь биоэнергетический спектр с самого начала (со стороны самых "коротких" метаболических источников) строился, исходя из "нулевых" запасов субстратов в организме спортсмена. И в то же время общеизвестным является факт подпитки организма при беге на сверхдлинные дистанции. Поэтому для решения поставленной задачи логичным будет принятие условия iсрв = 1 для последней, наиболее длинной дистанции, которую спортсмены высокого класса еще могут преодолеть без подпитки.

Практический опыт подсказывает, что такая дистанция находится в диапазоне между 40 и 20 км; то есть можно принять, что iсрв = 1 для дистанции 30 км. Такой выбор подкрепляется существенным биоэнергетическим доводом:

дело в том, что дистанция 30 км исчерпывает лишь мощность углеводно-липидного источника (I_N5-6 = 32,768 м [6], а в мощностном режиме еще можно бежать без подпитки.

Итак, граничные условия для кривой 4 (рис. 1) будут выглядеть следующим образом:

i₁ =3;

i₂ = 1;

I₁ = 100 м;

I₂ = 30 000 м;

Решив систему и получив показатели гиперболы, можем перейти к анализу последующих кривых.

Поскольку эти кривые связаны между собой методологической концепцией тренирующего воздействия, то следует применить совместный анализ, основанный на вышеупомянутой концепции. В данном случае удобнее всего связать анализируемые кривые в зоне спринтерских режимов, где имеется наибольшее количество проверенных исходных данных, на которые можно опереться.

Непосредственную связь рассматриваемых кривых позволяет осуществить номограмма (рис. 2), отображающая суть методологической концепции тренирующего воздействия и позволяющая получить максимальные значения i_t для любого тренировочного варианта, который может встретиться при проработке конкретного метаболического режима.

Таблица 1. Коэффициенты максимальной тренировочной интенсивности,%

Таблица 2. Основные показатели "предельных гипербол" для определения числа повторений (I_t)

В качестве примера на рис. 2 изображена номограмма для спринтерского креатинфосфатного режима E₃. По оси абсцисс откладывается диапазон для определения длины тренировочных отрезков, а по оси ординат - диапазон скоростей, выраженных в виде соревновательного темпа в беге на соответствующую дистанцию и представленных этой дистанцией.

В таком случае прямоугольник ABCD будет геометрическим местом точек, характеризующих максимальные значения параметра i, для любого сочетания длины отрезка и скорости пробегания. Для практического использования номограммы на прямоугольник ABCD наносится шкала для искомого параметра i_t.

Вершины прямоугольника соответствуют максимальным значениям i_t для рассматривавшихся выше принципиальных уровней интенсивности, связанных с методологической концепцией тренирующего воздействия. Одновременно эти локальные значения параметра i_t могут быть использованы для построения кривых на рис. 1.

Начнем с точки D, которой соответствует i_tmin то есть уровень максимальной тренировочной интенсивности.

Практика показывает, что для отрезков различной протяженности в качестве максимального тренирующего воздействия используются неодинаковые уровни интенсивности. Поэтому в расчет должен быть введен соответствующий параметр, который можно назвать коэффициентом максимальной тренировочной интенсивности - Кмти и который представляет собой процентное соотношение скоростей для рубежей t_i' и t_i (или I_i' и I_i).

Нами была разработана табл. 1, в которой приведены примерные значения такого коэффициента для различных метаболических режимов.

Учитывая, что, согласно данной таблице, для метаболического режима Е₃ коэффициент максимальной тренировочной интенсивности будет равен ~ 91%, то для предельного метрического параметра I_E3 = 64 м максимальный скоростной параметр на номограмме I_i' будет равен ~ 70 м.

Зная показатели гиперболы 4 (см. рис. 1), можно вычислить для I_E3 = 64 м величину параметра icpв. Его расчетное значение оказывается равным ~ 3,3.

Поэтому для I_E3 = 64 м в темпе 70 м можно принять i_tmin не более 4 раз. Таким образом, получаем значение it соответствующее точке D на номограмме, а также принципиальную точку на кривой 3 (см. рис. 1).

Далее переходим к точке С. Она соответствует варианту интенсивности I_i(I_i+1) или в данном случае бегу на 64 м в темпе 128 м, что составляет для мужчин-мсмк квазимаксимальную скорость. Повторный бег в последнем режиме фосфагенного диапазона приводит к снижению креатинфосфатных ресурсов организма. По этому поводу в специальной литературе описывается уровень критической концентрации КрФ в мышцах, ниже которого уже невозможно поддерживать максимальную скорость ресинтеза АТФ и, соответственно, невозможна работа максимальной мощности [1]. Там указывается, что при должных интервалах отдыха в одном тренировочном занятии можно произвести в данном режиме до 10-12 повторений до достижения уровня критической концентрации.

Принимаем для точки С i_tсрд =12; одновременно это дает нам характерную точку на кривой 2 (см. рис. 1).

Далее обратим внимание на следующее обстоятельство: линия на шкале для параметра i_t вышедшая из точки С, никогда не попадет в точку А. Причин этого по крайней мере две: во-первых, i_t для варианта I_i-1(I_i) не равно i, для варианта I_i(I_i+1), а во-вторых, точка А на номограмме соответствует даже не I_i-1(I_i), а I_i-1(I_i').

Примерной оценкой было установлено, что первая причина приводит к отклонению точки F от угла А примерно на 20% от AD. Отклонение из-за второй причины может быть оценено процентной величиной зазора между I_i' и I_i, определяемого с помощью Кмти. Учитывая, что для режима E₃, Кмти = 91% (см. табл. 1), процентная величина зазора между I_i' и I_i будет равна ~ 9%. Итого получается AF = 29% от AD.

Таблица 3. Число повторений (I,) предельных метрических отрезков (Iпр) метаболических режимов

В результате на номограмме появляется пунктирная линия CF , параллельно которой должна располагаться шкала параметра i_t. Далее соединяем точки В и D прямой линией;

после чего, зная метрическое расстояние GD и число шагов параметрической шкалы на этом отрезке, можно (заложив определенную нелинейность) вычислить остающееся число шагов на известном отрезке BG и получить, таким образом, параметр itmax соответствующий угловой точке В на номограмме и характерной точке на кривой 1 (см. рис. 1), Таким образом, для отрезка 32 м было получено i_tmax = 30.

Получив первую точку на кривой 1, вторую попытаемся найти среди стайерских дистанций. Известно, что бегуны, готовящиеся к суточным пробегам, для лучшей адаптации тренируются в ночное время. Поэтому вполне реален следующий тренировочный вариант: бег с 6.00 до 14.00, отдых - до 22.00 и бег с 22.00 до 6.00. Таким образом, в течение тренировочного дня (а точнее, суток) дважды повторяются отрезки временной протяженностью в 8 ч.

Согласно полному биоэнергетическому спектру [6] временной отрезок в 8 ч соответствует (для бегунов высшего уровня) предельному временному параметру t_N6. Но учитывая, что в данном случае нас интересует вариант t_i-1(t_i+1), супермарафонцам можно рекомендовать режим t_N6(t_N6-7). Поскольку t_N6-7 = 39:00, то за 8 ч можно преодолеть примерно 1/5 от I_N6-7 = 524, 288 м (или ~ 100 км).

Таким образом получаем вторую точку i_tmax = 2 для отрезка протяженностью в 100 км. Через две точки можно провести кривую 1 (см. рис. 1).

Для кривых 2 и 3 достаточно иметь по одной точке, так как их можно построить по принципу конгруэнтности к известным кривым 1 и 4.

Что касается построения аналогичных кривых для второго "предельного" контингента (т.е. мальчиков 10-летнего возраста), то сразу можно заметить: для этого контингента нет смысла разделять кривые для icpв и itmin. Трудно ожидать, что малолетние новички смогут сознательно воспроизводить интенсивность 90%. Поэтому для мальчиков 10 лет целесообразно ограничиться тремя кривыми: для itmax (кривая 5), itmin(кривая 7) и i_tсрд (кривая 6).

Первую точку для кривой itmin (она же icpв) найдем в спринтерском диапазоне. Известно, что единственной дистанцией, которую дети такого возраста преодолевают в соревнованиях дважды (забеги и финал), является бег на 30 м. Следовательно, i_tmin = 2 для отрезка 30 м.

Вторую точку находим на длинных отрезках. Для нее должно соблюдаться условие i_tmin = 1; кроме того, она должна соответствовать наиболее длинной (и в то же время посильной) соревновательной дистанции, позволяющей оценить стайерские способности юных бегунов.

В этом плане наиболее подходящей дистанцией выглядит бег на 800 м. Известно, что для раскрытия стайерских способностей весьма важен режим максимального потребления кислорода (МПК). Для мальчиков 10 лет предельный метрический параметр мощностной составляющей режима МПК равен I_N4-5 = 832 м [4]. Емкостный режим МПК для неподготовленных детей оказывается слишком тяжелым. В экспериментах, проводимых с данным контингентом, было выяснено, что предельным, сопровождающимся отказом от работы является именно такой рубеж [2]. Кстати, такой нагрузки оказывается достаточно для оценки перспективности будущих бегунов на выносливость по показателю МПК [10]. Итак, приняв i_tmin = 1 для I = 800 м, можно построить кривую 7.

Для построения кривой 5 обратимся вначале к спринтерскому диапазону. Согласно полному биоэнергетическому спектру для мальчиков 10 лет I_N3 = 13 м [4]. На основании многолетнего практического опыта для такого контингента в качестве оптимальной можно рекомендовать величину i_tmax = 4.

Вторую точку определим в стайерских режимах. Для такого возраста в качестве максимальной кроссовой пробежки можно рекомендовать дистанцию, у которой превалирующим вариантом энергообеспечения будет углеводный аэробный ресинтез АТФ, или в крайнем случае углеводно-липидный в мощностном варианте. Скажем, 3000 м в темпе 13 км (для сравнения - I_N5 = 3328 и I_N5-6 = 13.312 м [4]. Получим i_tmax = 1, для отрезка 3000 м можно построить кривую 5.

Зависимость Исрд = f(l) для мальчиков 10 лет (кривая 6) строим, используя конгруэнтность по отношению к предельным кривым 5 и 7, а также пропорциональность по отношению к пучку кривых для мсмк. Ориентировочной точкой является значение it = 3 для I = 20 м.

На основании полученных граничных условий можно составить системы уравнений и, решив их, получить основные показатели для каждой из семи гипербол, представленных на рис. 1. Основные показатели, соответствующие уравнению 2, сведены в табл. 2.

Число повторений отрезков. Зная показатели гипербол, можно рассчитать максимальные значения it, соответствующие характерным уровням интенсивности (или, другими словами, крайним пределам тренировочных диапазонов, отображенных в методологической концепции тренирующего воздействия).

В табл. 3 представлены максимальные значения числа повторений, соответствующие предельным метрическим параметрам метаболических режимов. Как было показано выше, эти значения необходимы для построения по каждому метаболическому режиму номограмм, позволяющих определить научно обоснованное максимальное значение i, для любого тренировочного варианта. В табл. 3 представлены расчетные (неокругленные) значения i, для более точного построения номограмм.

Анализ табл. 3 позволяет оценить практическое значение проведенного теоретического исследования. Во вступительной части данной статьи цитировались объемы нагрузок для ;

спортсменов высшего уровня, взятые из официального методического издания (20-40 повторений отрезков 100-400 м [9]).

Предположим, что меньшее число повторений относится к отрезку большей протяженности. И даже в этом случае усматривается разительное несоответствие полученных нами научных результатов официальным методическим рекомендациям. Если взять из табл. 3 значения предельных метрических параметров для мсмк, ближайшие к рассматриваемым отрезкам, и назначить самый неинтенсивный режим - I_i-t-I(I_i+1)), то получается I_tmax = 12 для I_N4 = 512 м и I_tmax = 19_N3-4 = 128 м. То есть вырисовывается примерно двукратное уменьшение общего количества повторений отрезков данного диапазона.

В детском и подростковом возрасте разница получается еще более существенной. Так, сравнение результатов расчета с поурочными программами для ДЮСШ и СДЮШОР 1986 г. показало, что там, где официальное методическое пособие рекомендует разовый тренировочный объем - 6-8 х 60 м, оказывается вполне достаточно 1-2 х 60 м.

Таким образом, сокращение числа повторений, получаемое на практике благодаря методу "предельных кривых", так же, как 1-й и 2-й принципы [6, 7], способствует уменьшению тренировочных объемов беговой нагрузки.

Кроме того, следует отметить еще один чрезвычайно важный результат проведенного исследования. До сих пор повторные тренировки применялись в тренировочном процессе для отрезков, протяженностью начиная от самых коротких и до 1-2 км. Предложенная в данной работе закономерность i_t = f(l) с математической очевидностью показывает и рекомендует включение в процесс беговой подготовки таких нагрузок, как повторный темповый бег, повторный кросс и даже, как было показано выше, повторные пробеги продолжительностью до 8 ч (см. табл. 3).

Выводы

1. Максимальное число повторений в одной тренировке (i_t) предельных отрезков (I) тренировочного диапазона каждого метаболического режима (для любого спортивно-квалификационного уровня) ограничивается гиперболами вида: i_t = aI^-b.

2. Максимальное число повторений для любого тренировочного варианта внутри конкретного метаболического режима может быть определено при помощи специальной номограммы.

3. Применение "метода предельных кривых" для определения максимального числа повторений беговых отрезков способствует оптимизации данного параметра, что, в свою очередь, приводит к уменьшению тренировочных объемов беговой нагрузки.

4. Закономерность i_t = f(l) доказывает целесообразность применения темповой и кроссовой беговой нагрузки в повторном варианте.

Литература

1. Биохимия. Учебник для институтов физической культуры. Под ред. В.В. Меньшикова, Н.И. Волкова. - М.: ФиС, 1986.

2. Голощапов Б.Р., Прокудин Б.Ф. Оптимизация нагрузок при непрерывном беге на этапе предварительной спортивной подготовки младших школьников. "Теория и практика физической культуры", 1982, № 7, с. 28-29.

3. Офицеров Ю.Д., Смирнов М.Р. Методологическая концепция тренирующего воздействия на метаболический источник. "Теория и практика физической культуры", 1994, № 5-6, с. 21-23.

4. Смирнов М.Р. Еще раз о "зонах относительной мощности". "Теория и практика физической культуры", 1991, № 10 с. 2-9.

5. Смирнов М.Р. Закономерности биоэнергетического обеспечения циклических нагрузок (на примере легкой атлетики). Монография. - Новосибирск: изд-во НГПУ, 1994.

6. Смирнов М.Р. Принцип избирательности режимов циклической нагрузки. "Теория и практика физической культуры", 1993, № 3, с. 2-6.

7. Смирнов М.Р. Принцип последовательной реализации режима. "Теория и практика физической культуры", 1994, №11, с. 39-43.

8. Смирнов М.Р. Связь основных параметров беговой Нагрузки с энергетическим метаболизмом. "Теория и практика физической культуры", 1990, № 7, с. 18-26.

9. Учебник тренера по легкой атлетике /Под ред. Л.С. Хоменкова. Изд. 2-е. - М.: ФиС, 1982.

10. Фарфель B.C., Коц Я.М. Физиология человека. - М.: ФиС, 1970.

Поступила в редакцию 15.11 95

  На главную    В библиотеку    Обсудить в форуме 

При любом использовании данного материала ссылка на журнал обязательна!