|
Abstract FORTHCOMING MATCH-COMPUTER VERSION A.A. Polozov Faculty of physical culture of the Ural state technical university (Ural politechnical institute) Key words: rating, effectiveness of a game, tactics. The article is devoted to the modelling a possible variant of forthcoming match. This is reached by the receiving the follows: 1. Universal pedagogical actions of rivals estimation by their participation in dynamics attacks, receiving on that base by means of the system of linear equations of estimation the players. Estimation allows to get the result of the resisting any pairs of rivals - participants of match. 2. Games's algorhythm. Tactics of the game they understand as the ways of redistribution the play load in the benefit the stronger partners on the postions of weakerivals. The efficacy of participant's game is characterized by the degree of realisation such direction of the game. That allows to control the changes during the game, and becomes the determing factor in the possibility of creation a computer version. 3. The player receives a possibility to develope the technic-tactical mentality. He can observe of the possible development of events and by means of the "mouse" to interfere the game gradually making it more effective. The model carries the universal character for playing kinds of sport.
|

ПРЕДСТОЯЩИЙ МАТЧ. КОМПЬЮТЕРНАЯ ВЕРСИЯ А.А. Полозов* Ключевые слова: рейтинг, эффективность игры, тактика. Статья посвящена моделированию возможного варианта предстоящего матча. Рассмотрим данную тему на примере футбола. Вероятность забить мяч в ворота соперников из данной позиции в общем случае прямо пропорциональна вертикальному (a) и горизонтальным (b) углам, под которыми видны ворота из данной точки поля, и обратно пропорциональна времени (т) полета мяча до них (т.е. расстояние r, деленное на скорость (v) полета мяча). Каждой точке поля можно приписать определенное значение индекса (ф), равного ab/r, зависящего только от расположения точки относительно ворот. В ряде видов спорта (волейбол, бадминтон) более уместно использовать отношение расстояния до точки падения мяча, волана к т. Если выделить точки равного индекса, то они расположены радиально относительно ворот и представляют деформированный шар. Действия атакующих направлены внутрь этого шара. Назовем сравнительной результативностью (R) усредненную по всем играм данного турнира долю забитых мячей с точек данного ф: R = 1 - exp (-a x ф). Выделим в атакующей игре
футболистов следующие элементы игры и дадим их
краткую характеристику:
(1) или в виде
(2), где i - свои игроки, j - чужие; Rт,
Rтi - рейтинг команды и игрока, где - Аналогично (2) получают
равенство для каждого игрока по его участию в
позитивных ( Проблема в том, что нагрузка по игре в атаке и в обороне среди игроков распределяется неравномерно. Для нивелировки этого фактора приходится считать среднее по всем партнерам участие в ДА по игре в атаке (N ат) и обороне (N об) и доумножить в - приведенные ранее З, П, R+, R- соответственно на N ат/Ni и на N об/Ni. Аналогично (2) рейтинг игрока может быть разложен на базовые рейтинги (по соответствующим компонентам ДА). Далее их называем параметрами. Более подробно тема ДА рассмотрена в (1). Основная проблема, над которой ежедневно ломают голову тренеры, - поиск наиболее эффективной игры. Вырабатываемая ими тактика - это способы перераспределения игровой нагрузки в пользу более сильных своих (i) на позиции наиболее слабых чужих (j) игроков. Т.е. одна задача распадается на две. Назовем эффективностью игры Эi игрока i: Эi = (3) Игрок может "заработать"
большее Эi( (4)
(5) Однако аналогично действуют и
соперники. Значит,
(6) Эффективность работы тренера
определяется Э его команды или просто разницей
Rтi его команды и среднего Rт его игроков. В идеале
необходимо стремиться в каждой атаке выводить
наиболее сильного партнера на наиболее слабого
соперника. Однако проблема в том, что его Rт при
такой перегрузке неизбежно будет
экспоненциально падать. Причем если при
небольших нагрузках велика доля энергозатратных
параметров (обводка), то при больших нагрузках
возрастает доля менее затратных (позитивный пас).
Сложность в том, что нагрузка по одному параметру
всегда идет на фоне других. Исследование
видеозаписей матчей команд высшей лиги по
мини-футболу показывает аналогичную зависимость
и по параметрам ( Rтi = Rтiо х exp(A1х (7) Здесь А1-4 - коэффициенты,
нивелирующие разноплановые нагрузки. Набирая
информацию по различным сменам (они, как правило,
отличаются по
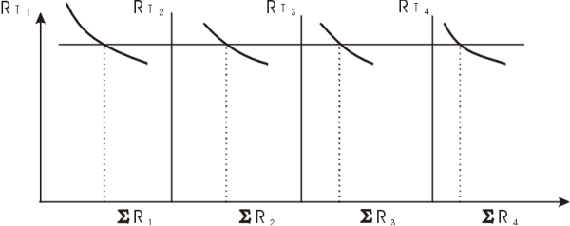
Назовем эквипараметрическим режимом такое распределение нагрузок среди партнеров, при котором их рейтинги оказываются равными. Это значит, что нагрузка перераспределяется в пользу наиболее сильных партнеров до тех пор, пока их Rт не снизятся до повысившихся Rт более слабых партнеров. Имеющиеся по всем игрокам зависимости (7) расставляют в порядке убывания Rтiо и методом последовательных приближений находят такое значение Rт, при котором суммарная нагрузка равна матчевой (см. рисунок). При этом не исключено, что часть игроков окажется без нагрузки. Это позволяет, например, в "сменных" видах спорта обходиться меньшим числом игроков. Таким образом, эффективность игры команды зависит от умения каждого игрока выдерживать необходимые пропорции по нагрузкам в игре, не упускать по ходу игры выгодный размен в атаке и добиваться пропорциональных разменов в обороне. Однако этого трудно добиться одним объяснением, лучше всего эту сложную задачу решить в привычном для игрока игровом режиме - в виде компьютерной игры. Для этого осталось решить еще одну проблему. Из (1) следует, что
(8) Если К = 1 - exp(-a x (R2 - R1) / N). (9) Компьютерная версия
предстоящего матча представляет собой
воспроизведение возможной картины игры на
основе полученных через решение систем линейных
уравнений данных (Rтi, Rтiо, Рейтинг игрока в ходе игры
считается из (2), где используются изначально
заданные Rт партнеров и соперников, фактические Далее определяется - каким он
должен быть на оставшемся отрезке игры, чтобы в
итоге он соответствовал изначально заданному. И
этим текущим значением реформируют v. Аналогично
поступают с Эi и К. В более "жесткой" версии
перебирают все возможные варианты продолжения в
зоне ДА с определением возможной точки удара (R x v1
x v2...), аналогично учитывают возможные ответы
соперника при потерях мяча, формируют на этой
основе Все расчеты ведут на момент получения игроком мяча. Игроку предоставляется возможность не просто наблюдать за возможным развитием событий, а с помощью "мыши" вмешиваться в игру, постепенно делая ее более эффективной. Структура компьютерной версии для других видов спорта во многом аналогична. * А.А. Полозов. Система рейтинга в игровых видах спорта и единоборствах.- Екатеринбург: УГТУ-УПИ, 1995. Поступила в редакцию 20.08.96
При любом использовании данного материала ссылка на журнал обязательна! |