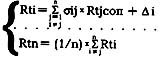ТЕХНОЛОГИИ СПОРТИВНОЙ ТРЕНИРОВКИ

Abstract

PERSONAL CONTESTATION IN TEAM SPORT KINDS WITHOUT MUTATION OF THE GAME STRUCTURE

A.A. Polozov V.F. Shcherbakova

Ural state technical university, Ekaterinburg

Ural pedagogical  institute, Ekaterinburg

Key words: ranking, micromatch, microtournament, macrotourna-ment.

It is proposed the form of doing of the personal contestaton in all the team sport kinds without mutation of the game structure. It is attained by doing of the series of micromatches under teams with different partaker contents with the count, that is usual for the given sport kind. Each partaker plays equal count times as with the robust partners, as with the feeble these, be is in the equal conditions with outher, but the total result corresponds to the results of his team in the micromatches. They are found the uniform allocations as among the partners, as among the contenders with the theoretical minimal count of the micromatches for all the team sportkinds. They are stated the interpretation principles for the taken results of macrotourna-ment.

ЛИЧНОЕ ПЕРВЕНСТВО В КОМАНДНЫХ ВИДАХ СПОРТА БЕЗ ИЗМЕНЕНИЯ СТРУКТУРЫ ИГРЫ

А.А. Полозов, В.А. Щербакова

Уральский государственный технический университет
Уральский педагогический институт

Ключевые слова: рейтинг, микроматч, микротурнир, макротурнир.

Назовем рейтингом смещенный в область целых положительных чисел результат участника всеобщего гипотетического кругового макротурнира. Построение шкалы рейтинга основано на следующих принципах:

1. Приоритет гола над очком. (В данной работе можно использовать и очки (М, N) и голы (3, П) - преобразования аналогичны.)

2. Для расчетов выбрана функция Д = 1000 х (3-П)/(3 + П), дающая минимальное отклонение результатов личной встречи соперников от разницы их общетурнирных показателей.

3. Принцип транзитивности. Позволяет не играть каждому с каждым, экстраполируя часть результатов на все остальные игры макротурнира.

4. Принцип асимптотической устойчивости. Предполагает, что полученным результатам может соответствовать единственное решение - значение рейтинга. Предлагается использовать систему линейных уравнений (СЛУ), где коэффициенты при неизвестных рейтингах - ij - доля совместной i - j активности в общей (= 1), а свободный член - i. Однако такая система имеет множество решений. Возьмем заполненную турнирную таблицу и вычеркнем из нее строку. Из оставшихся результатов можно легко восстановить потерю, а вот при второй вычеркнутой строке теряется результат встречи между собой. Для обеспечения единственности решения в полученной системе одно любое уравнение заменяется другим, задающим средний рейтинг микротурнира. Или к полученной системе просто добавляется это уравнение. Решение будет тем же.

5. Принцип трансляции в глубину. Обеспечивает универсальность принципов пересчета рейтинга при переходе с макроуровня на последующие слои микроуровней. Позволяет трансформировать рейтинг команды на рейтинги составляющих ее игроков, рейтинги игроков - на рейтинги игроков по базовым компонентам игры; дает возможность замены нескольких соперников одним, им эквивалентным.

6. Принцип корректировки среднего рейтинга макротурнира. Более подробно принципы построения шкалы рейтинга изложены в [1, 2]. Для любого произвольного микротурнира игроков возможно получение соответствующей СЛУ. Это так называемое "общее" решение:

Главное требование в личном первенстве - это привычный для игрока игровой режим на привычной позиции. Однако при произвольном режиме его очень трудно выполнить. Основное преимущество общего решения - возможность гибкого перестроения режима проведения игры под заданные условия. При этом для обработки полученных данных необходимо решать соответствующую СЛУ общего вида. Поэтому предлагается такой вариант проведения личного первенства, при котором распределение равномерно как по партнерам, так и по соперникам. Это позволяет тривиально, прямым вычислением, решать СЛУ микротурнира, придать ему необходимую организационную форму, получить привычную ритмичность игры, играть на привычной позиции. Равномерность распределения позволяет подставить новое n + 1 уравнение, задающее средний рейтинг микротурнира, в предыдущие п. При этом в уравнении остается только один неизвестный рейтинг - R_Ti. Тогда из равенства (2) следует:

Ожидаемое количество микроматчей в личном первенстве можно заранее рассчитать. Для этого принимаем число участников равным минимальному, при котором можно проводить двустороннюю игру. Затем определяем минимальное целое количество циклов, при котором все игроки могут быть партнерами и аналогично - соперниками. Далее ищем число микроматчей, при которых они сходятся. Для распределения 2х2 число игр равно трем. В мини-футболе минимальное число участников с обеих сторон - восемь. При распределении 4х4 i-игрок играет с каждым из 7 партнеров равное количество игр. Минимальное их число равно 2 1/3. То есть, например, в первом микроматче 1-й играет со 2, 3, 4-м, во втором-с 5,6,7-м, а на третий остается только один 8-й игрок. Значит, минимальное целое число игр равно семи - 2 1/3 х 3 = 7. Могут ли в такое же число игр "уложиться" соперники? Их минимальное число игр равно 1,75. Например, в первом микроматче - соперниками 1-го игрока могут быть игроки 2,3,4,5-й, во втором - 6, 7 и 8-й. Баланс равен: 21/3х3= 7 = 1,75х4. Ожидаемое число микроматчей при распределении 4х4 равно семи. С каждым из партнеров i-игрок играет 3 раза, а против него - 4. При соотношении 5х5 баланс равен 2,35х4 = 9 = 1,8 х 5. Но получить такое распределение невозможно. Вели начать построение распределения с игроков 1,2, 3-го..., то уже на 3-м оно прекращается, поскольку невозможно расположить 3-го игрока по микроматчам так, чтобы не нарушить баланса с 1-ми 2-м (4 раза - партнеры, 5 - соперники). В этой ситуации для распределения 5х5 приходится выбирать вариант с числом игр, равным 18. Для соотношения 6х6 баланс равен 2,2х5= 11 = 11/6 х 6. Число игр равно 11. Для соотношения 10 х 10 баланс равен 19/9x9 = 19 = 1,9x10. Число игр равно 19. Для 2х2 распределение выглядит так:

1. 1 2 / 3 4

2. 1 3 / 2 4

3. 1 4 / 2 3

(3R_T(l) + Rt(2) + R_T(3) + R_T(4))/6- (2R_T(2) + 2R_T(3) +2R_T(4))/6=i

Для 4х4:

R_Ti = RT сp. + 3,5хi

1. 1 2 3 4 / 5 6 7 8

2. 1 2 5 6 / 3 4 7 8

3. 1 2 7 8 / 3 4 5 6

4. 1 3 5 7 / 2 4 6 8

5. 1 3 6 8 / 2 4 5 7

6. 1 4 5 8 / 2 3 6 7

7. 1 4 6 7 / 2 3 5 8

Для 5х5:

R_Ti = R_T ср. + 4,5 x i

1. 1 2 3 4 5 / 6 7 8 9 10

2. 1 2 3 6 8 / 4 5 7 9 10

3. 1 2 3 7 9 / 4 5 6 8 10

4. 1 2 4 7 8 / 3 5 6 9 10

5. 1 2 4 6 10 / 3 5 7 8 9

6. 1 2 5 6 9 / 3 4 7 8 10

7. 1 2 5 7 10 / 3 4 6 8 9

8. 1 2 8 9 10 / 3 4 5 6 7

9. 1 3 5 7 8 / 2 4 6 9 10

10. 1 3 4 6 9 / 2 5 7 8 10

11. 1 3 4 5 10 / 2 6 7 8 9

12. 1 3 6 7 10 / 2 4 5 8 9

13. 1 3 8 9 10 / 2 4 5 6 7

14. 1 4 5 8 9 / 2 3 6 7 10

15. 1 4 6 7 8 / 2 3 5 9 10

16. 1 4 7 9 10 / 2 3 5 6 8

17. 1 5 6 7 9 / 2 3 4 8 10

18. 1 5 6 8 10 / 2 3 4 7 9

Для 6х6:

R_Ti = R_T ср. = 5,5 хi

1. 1 2 3 4 9 11 / 5 6 7 8 10 12

2. 1 2 3 5 7 8 / 4 6 9 10 11 12

3. 1 2 6 8 9 10 / 3 4 5 7 11 12

4. 1 2 4 7 10 12 / 3 5 6 8 9 11

5. 1 3 6 7 9 12 / 2 4 5 8 10 11

6. 1 3 8 10 11 12 / 2 4 5 6 7 9

7. 1 3 4 5 6 10 / 2 7 8 9 11 12

8. 1 4 5 8 9 12 / 2 3 6 7 10 11

9. 1 5 7 9 10 11 / 2 3 4 6 8 12

10. 1 2 5 6 11 12 / 3 4 7 8 9 10

11. 1 4 6 7 8 11 / 2 3 5 9 10 12

Для 10х10:

R_Ti= R_T ср. + 9,5 x i

1. 1 2 3 4 5 6 7 8 9 10 / 11 12 13 14 1516 17 18 19 20

2. 1 2 3 4 5 11 12 13 14 15 / 6 7 8 9 10 16 17 18 19 20

3. 1 2 3 6 8 14 15 16 19 20 / 4 5 7 9 10 11 12 13 17 18

4. 2 3 7 9 12 15 17 18 19 / 4 5 6 8 10 11 13 14 16 20

5. 2 4 7 8 11 12 16 17 20 / 3 5 6 9 10 13 14 15 18 19

6. 2 4 6 10 12 13 18 19 20 / 3 5 7 8 9 11 14 15 16 17

7. 2 5 6 9 11 14 17 18 20 / 3 4 7 8 10 12 13 15 16 19

8. 2 5 7 10 13 14 16 17 19 / 3 4 6 8 9 11 12 15 18 20

9. 2 8 9 10 11 13 15 16 18 / 3 4 56  7 12 14 17 19 20

10. 1 3 5 7 8 11 13 18 19 20 / 2 4 6 9 10 12 14 15 16 17

11. 1 3 4 6 9 11 13 16 17 19 / 2 5 7 8 10 12 14 15 18 20

12. 1 3 4 5 10 15 16 17 18 20 / 2 6 7 8 9 11 12 13 14 19

13. 1 3 6 7 10 11 12 14 16 18 / 2 4 5 8 9 13 15 17 19 20

14. 1 3 8 9 10 12 13 14 17 20 / 2 4 5 6 7 11 15 16 18 19

15. 1 4 5 8 9 12 14 16 18 19 / 2 3 6 7 10 11 13 15 17 20

16. 1 4 6 7 8 13 14 15 17 18 / 2 3 5 9 10 11 12 16 19 20

17. 1 4 7 9 10 11 14 15 19 20 / 2 3 5 6 8 12 13 16 17 18

18. 1 5 6 7 9 12 13 15 16 20 / 2 3 4 8 10 11 14 17 18 19

19. 1 5 6 8 10 11 12 15 17 19 / 2 3 4 7 9 13 14 16 18 20

Каждый участник играет одинаковое число раз как с сильными, так и со слабыми партнерами, находится в равных условиях с другими, а итоговый результат соответствует результатам его команды в микроматчах. Использование фиксированных коэффициентов предполагает равную активность участников, чего может не быть на практике. Для этого предпочтительнее использовать голевые соотношения и играть микроматч до определенной суммы забитых и пропущенных мячей. Если при этом микроматч выходит из привычного режима, то постепенно сокращают численность обеих сторон. Для 10х10 в А предпочтительнее использовать очковые соотношения. Из полученных результатов микротурниров формируют усредненную сезонную оценку уча-стника макротурнира.

Разница в рейтинге Иванова и Петрова соответствует результату встречи команд, состоящих только из Ивановых и только из Петровых.

Из полученных результатов макротурнира можно сформировать диаграмму распределения рейтинга по любому фактору и потом его нивелировать. Так можно компенсировать, например, демографический фактор в соревнованиях сборных. Или из результатов двух макротурниров можно получить последовательность изменения среднего рейтинга в узких возрастных группах участников обоих макротурниров при их выходе из одной группы в другую с последующими сглаживанием, экстраполяцией результатов на один возраст и соответствующей компенсацией в итоговой оценке. Тогда и в 50 лет можно будет стать чемпионом мира.

Литература

1. Полозов А.А. Система рейтинга в игровых видах спорта и единоборствах. - Екатеринбург: УГТУ - УПИ, 1995. - 110 с.

2. Полозов А.А. Рейтинг-формула //Теория и практика физической культуры, 1996, № 1, с. 58.

Поступила в редакцию 07.08.97

  На главную    В библиотеку    Обсудить в форуме 

При любом использовании данного материала ссылка на журнал обязательна!
 

Реклама: