Abstract PROBLEMATIC- STRUCTURAL METHOD OF TRADITIONAL KARATE-DO MULTIMEDIA COMPETITIONS MODELING O.B. Dmitryev, chairman of attestation commission of national Russian "Karate-Do Fudokan" federation V.A. Shirokov, Ph.D P.K. Petrov, Ph.D, lecturer Udmurtian State university, Izhevsk Key words: multimedia, referees, software users, Karate-Do tournaments, modeling, training Traditional Karate-Do referee's instructing is very laborious and expensive process. The author suggests a problematic-structural method of traditional Karate-Do multimedia competitions modeling for virtual tournaments building. Users can reach the required volume of referee's practice and rise the qualification level up to the mastership by this method. The given method allows to prune essentially the financial, labor, temporal expenses for referee's effective training.
|

МЕТОД ПРОБЛЕМНО-СТРУКТУРНОГО МОДЕЛИРОВАНИЯ МУЛЬТИМЕДИА СОРЕВНОВАНИЙ ПО ТРАДИЦИОННОМУ КАРАТЭ-ДО Председатель ВАК национальной
Российской федерации "Каратэ-до Фудокан",
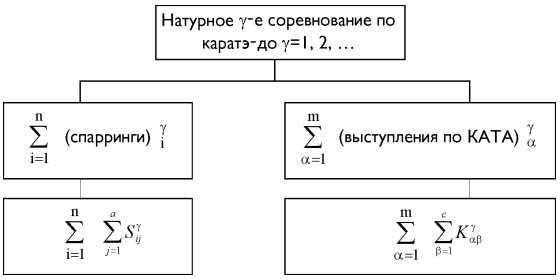
аспирант О.Б. Дмитриев Удмуртский государственный университет, Ижевск Ключевые слова: каратэ-до, традиционное каратэ-до, мультимедиа, компьютерное моделирование, судейство соревнований, правила соревнований, мультимедиа соревнования. В настоящее время большое внимание уделяется вопросам использования математических и мультимедийных моделей в качестве инструмента исследования, преобразования и имитации сложных систем и динамических процессов [1-3]. Быстрое развитие вычислительной техники позволило резко увеличить сложность применяемых моделей и использовать возможности мультимедиа при моделировании процессов. Подготовка судей по традиционному каратэ-до и повышение их квалификации - трудоемкий и дорогостоящий обучающий процесс, требующий от судей постоянной практики судейства, особенно на турнирах высокого ранга. Возникает противоречие между требованием интенсивности судейской практики и необходимыми для этого временными и финансовыми затратами. Для устранения данного противоречия предлагается создавать и использовать компьютерные турниры на базе проблемно-функциональных компьютерных библиотек ситуаций (видеофрагментов) соревнований по традиционному каратэ-до и применения метода структурного мультимедиа моделирования. При этом пользователь на своем учебном компьютерном месте может достигать необходимой интенсивности практики судейства мультимедиа соревнований. Суть проблемного мультимедиа моделирования соревнований по каратэ-до заключается в структурной перестройке и имитационном воспроизведении реальных натурных соревнований в компьютерной среде с целью формирования множества новых мультимедийных соревнований. Схема процесса формализации соревнований имеет вид:
где
i=1, 2, .., n; n - количество
спаррингов в
j=0, 1, 2, .., a; 0 - индекс фрагментов, соответствующих началу поединков; а - количество возможных ситуаций в спарринге, предусмотренных правилами;
S и K - соответственно множества видеофрагментов по КУМИТЭ и КАТА (практически соответственно систематизированные проблемно-функциональные ЭВМ - видеобиблиотеки по КУМИТЭ и КАТА). Модель мультимедиа соревнований представляет собой функциональную конечную последовательность:
(1) или где М - множество видеофрагментов по КУМИТЭ и КАТА (практически проблемно-фун кциональная библиотека видеофрагментов по КУМИТЭ и КАТА); Р - количество элементов Мn, необходимое для моделирования соревнований. Замечание 1. Мультимедиа
соревнования по КУМИТЭ и КАТА имеют одну и ту же
структурную модель (1). Задавая при моделировании
различные данные Замечание 2. Модель мультимедиа спарринга составляет основу мультимедиа соревнования по КУМИТЭ. Ниже мы будем рассматривать модель спарринга. Значения элементов Мn (последовательность составляющих видеофрагментов мультимедиа модели) определяются двумя способами: 1. Значения коэффициентов
2. Значения коэффициентов
Чтобы модель функционировала,
необходимо задать исходные данные, начальные и
конечные условия для спаррингов и для турнира в
целом, граничные условия для видеофрагментов
(условия связки элементов Исходными данными являются
видеозаписи фрагментов натурных соревнований по
каратэ-до ( Элемент
Для каждого видеофрагмента Начальные и конечные условия
задаются для переменных моделирования (t, 1) t - чистое время спарринга (в соответствии с правилами tнач=0 : tкон=90 с). Для увеличения интенсивности и динамичности КУМИТЭ время мультимедиа спарринга должно быть меньше времени обычного спарринга (например, tкон=40 с или tкон=60 с); 2) Данная переменная может не отслеживаться, так как пользователь имеет возможность остановить спарринг при выполнении условия (4); 3) начальным условием для мультимедиа спарринга является видеофрагмент при t=0
где 4) конечным элементом модели мультимедиа спарринга является видеоэлемент "СОРЕ МАДЕ", соответствующий условию конца поединка: t=tкон или т.е. Начальные и конечные условия
для мультимедиа выступления по КАТА задаются в
каждом элементе Так как мультимедиа
моделирование соревнований является
разновидностью моделирования сплошных сред и
процессов, то для составляющих элементов модели
задаются граничные условия. Каждый
видеофрагмент мультимедиа соревнований по
КУМИТЭ Пользователь является активным участником моделируемых мультимедиа соревнований в качестве судьи (ФУКУ-СИН) или рефери (СУ-СИН). Обучаемый, как ФУКУ-СИН, оценивает смоделированную ситуацию и комментирует ее, используя условные обозначения судейских жестов. В качестве СУ-СИН пользователь оценивает мультимедиа спарринг и действия судей на мониторе, а затем выносит решение и заполняет протокол (функции арбитра - КАН-СА). Примечания: 1. Мультимедиа соревнование по КУМИТЭ является совокупностью мультимедиа спаррингов. 2. Метод проблемно-структурного моделирования позволяет перестраивать и компоновать каждое отдельное мультимедиа выступление по КАТА аналогично модели мультимедиа спарринга. Выводы Метод проблемно-структурного моделирования позволяет: 1. Создавать мультимедиа соревнования разного ранга, высокой информационной насыщенности и динамики поединков. 2. Моделировать мультимедиа соревнования в соответствии с некоторым управляющим заданием (для проведения экзаменов и контролирующих аттестаций). 3. Увеличить интенсивность судейской практики пользователя. 4. Сократить финансовые, трудовые и временные затраты, необходимые для повышения квалификации судей. Литература 1. Голев Р.В., Попов В.М., Дмитриев О.Б. Автоматизированный комплекс формирования, анализа и реализации математических моделей динамики технических систем. В кн.: Тезисы докладов Четвертой всесоюзной конференции "Автоматизация поискового конструирования и подготовка инженерных кадров", АПК-87. Волгоград, 1987, с. 65. 2. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. 2-е изд. - М.: Энергоатомиздат, 1988. - 480 с. 3. Аврамчук Е.Ф., Вавилов А.А., Емельянова С.В. и др. Технология системного моделирования /Под общ. ред. С.В. Емельяновой и др. - М.: Машиностроение. - Берлин: Техник, 1988. - 520 с.
При любом использовании данного материала ссылка на журнал обязательна! |
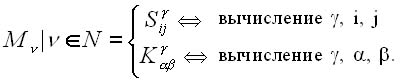 (2)
(2) (3)
(3)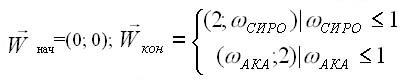 . (4)
. (4)