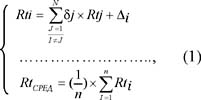НАЗАД

СОДЕРЖАНИЕ

ЕСЛИ БЫ ЕВРО-2000 ИГРАЛИ В КРУГ, ТО...

Кандидат педагогических наук А.А. Полозов

Уральский Государственный технический университет, Екатеринбург

Напомним, что рейтинг - смещенный в область целых положительных чисел результат участника всеобщего гипотетического кругового макротурнира (1). Представьте себе турнирную таблицу, в которой перечислены все участники макротурнира из всех стран. Немцы, итальянцы, голландцы... Создать целиком заполненную таблицу макротурнира нереально. Но можно все эти результаты "свернуть" в уровень игры участников, нанесенный на шкалу рейтинга. Это удобнее. А потом, если необходимо, снова "развернуть" в виде результатов игр. При этом можно получить результаты всех, в том числе и не состоявшихся игр. Покажем это на примере прошедшего недавно Чемпионата Европы 2000 года по футболу. Сначала получим рейтинги из системы линейных уравнений (СЛУ) по (1).

где З и П - забитые и пропущенные мячи, _j = (Зij+Пij)/(Зi+Пi), і = (Зі - Пі)x1000/(З + П), Rt сред = 2000. Поскольку сборная Дании не сумела забить ни одного гола в ворота соперника, о ней можно сказать только, что она слабее своих соперников более чем на 1000 позиций.

Далеко не каждое распределение участников по шкале рейтинга можно считать корректным. Если А сыграла с Б со счетом 3:2, а В с С - 3:1, то погрешность определения = 1000/(3+2) + 1000/(3+1) = 450. Это вдвое больше, чем нужно для достоверного определения результата личной встречи А и С. Значит, должен существовать еще канал от А до С через Д. Две двойные связи заменят личную встречу. Или три тройные. Или по совокупности. Иными словами, (А, С) должна соответствовать значению 1000, деленной на среднюю результативность встречи. В общий список итогов макротурнира можно включать только тех участников, для которых это условие корректности взаимно выполняется при условии, что разница в их рейтингах не превышает 1000 позиций. Однако в рамках олимпийской системы о достоверности результатов можно только мечтать. Тем не менее назначение следующих встреч турнира должно идти в направлении равномерного снижения l по всем парам участников.

После того как определены рейтинги 15 оставшихся участников, можно было бы сразу определить результаты их личных встреч:

Rti - Rtj = = (З - П) ґ1000 / (З + П), (2)

Для этого упрощенно можно просто подставить на место (З + П) среднюю результативность всех встреч (2,75). Однако правильнее было бы составить еще одну СЛУ с участием результативности (Рез) участников:

{ Ni x Рез i + Рез j = (Зi + Пi), (3)

где Ni - число матчей, сыгранных i участником, (Зi + Пi) - сумма забитых и пропущенных им мячей во всех матчах, j - все соперники i на данном турнире. Полученные значения результативности (Рез i + Рез j) следует подставить в (2) вместо (З + П). Тогда результат встречи будет учитывать результативность обеих команд. Полученные результаты (официальные - вверху и вычисленные - внизу) представлены в таблице. Особо отметим, что они соответствуют среднему уровню выступления команд и всегда вариативно отличаются от конкретных итогов. Счет 0:0 равносилен тому, что команды вообще не играли. Это не равный счет, а нулевая неопределенность в соотношении сил. В конце таблицы приведены предполагаемые итоги турнира. Они определены из той логики, что чемпион - 1, проигравший чемпиону в финале - 2, проигравший в полуфинале - 3, проигравший в полуфинале 2-му месту - 4 и так далее. Примем результаты полученного кругового макротурнира как эталонные и оценим их среднее значение отклонения от официальных итогов. Оно равно 2,6 места. То есть если Вы играете на 5-е место, то можете занять 2-е. А если на 1-е, можете занять 4-е. При 15 участниках такая погрешность (далее сходимость ) составляет 83%. Вроде бы это не очень много для рокировок в глубине турнирной таблиц, но такая погрешность на уровне фаворитов турнира всегда воспринимается весьма болезненно.

Как, не меняя формулы розыгрыша, тем не менее без структурных изменений игры приблизить результаты турнира к результатам кругового турнира, который считается эталонным? Средняя разница по 28 играм в рейтинге составляла 210 позиций, что при средней результативности 2,75 соответствует преимуществу в счете 1,66:1,09. Упрощенно это значит, что в 0,66x0,09 случая счет 2:1 выиграет сильнейший, в 0,66x0,91 и 0,34x0,09 будет ничья 2:2 или 1:1 и в 0,34x0,09 случая будет поражение 1:2. Если предположить это противостояние в рамках олимпийской системы и шансы на пенальти 50:50, то сильнейшие одержат верх в 78% случаев. Если число участников также 16 и в основе их стартового распределения лежит слепая жеребьевка, то при числе туров равном 4 сходимость оценки будет (0,78)⁴ x 100 = 37%. То есть смысла играть в таком турнире нет. Если жеребьевка направлена на сведение вначале сильнейших и слабейших, то в первом и втором турах сходимость будет на уровне 100%. Однако, даже здесь в лучшем случае (0,78)² x 100 = 61%. Допустим теперь, что турнир идет не по олимпийской системе, а по последовательно-зональной, то есть начинают в подгруппе из 4 команд, затем по два победителя выходят в две полуфинальные четверки и затем - финальная четверка. Это равносильно увеличению соотношения с 1,66:1,09 до 5,0:3,27. Такое противостояние выявляет победителей с преимуществом в 1-2 мяча, что почти гарантирует 100%-ную сходимость в подгруппе. Но нет никаких гарантий, что на старте все подгруппы окажутся равноценными и именно этим при данной результативности в большей степени определяется сходимость итогового распределения мест с чисто круговым, тем более что, как и при олимпийской системе, предыдущие результаты "забываются" на следующей стадии. Сходимость в таких случаях редко бывает выше 85%. Швейцарская система решает все эти проблемы, но по ряду причин 100% не достигает.

Есть иной путь. Это путь совершенствования структуры игры в рамках действующих формул с задачей повышения достоверности полученных результатов. Игра и правила должны находиться в динамичном равновесии. Несправедливо, когда команды типа сборной Италии или Норвегии, виртуозно используя все возможные издержки правил игры и организации соревнований, незаслуженно добиваются более высоких мест. Футбол просто перестанет быть спортом номер один, если все команды будут проводить матч на своей половине поля в ожидании ошибки соперника или пенальти. Необходимо также препятствовать увеличению доли "неигровых" голов из стандартных положений, настаивая на выявлении победителя на основе "игрового" голевого превосходства. Заслуживают одобрения те изменения правил, которые значит ельно снижают влияние судей на результат. Пенальти и положение вне игры стали стоить слишком дорого. Было бы целесообразно:

1. Использовать более быстро летящие мячи с возможно меньшим отскоком.

2. Фиксировать фолы. При этом при первом фоле при пробитии с места нарушения один игрок обороняющейся команды обязательно находится на чужой половине поля (за центром поля), при втором - 2 игрока и так далее.

3. Играть матч до некоторой суммы забитых и пропущенных мячей, например до трех, и потом ее закончить. Кто сколько забил - столько очков и получил. Если игра затягивается (более 90 мин), то постепенно сокращать численность сторон (например, через 5 мин, в паузах, тренеры отзывают по одному игроку).

4. Сузить поле действия правила "положения вне игры".

5. Увеличить число судей по периметру игры и назначать двух главных судей.

6. Отменить пенальти. Вместо них назначать штрафные с места нарушения.

Вопрос о формуле турнира - это не вопрос о том, какому числу участников она нравится, а какому нет. Это чисто расчетный вопрос, который правильнее решать определением рейтингов участников и их результативности, исходя из предыдущих достижений и предположительного расчета сходимости предлагаемой формулы. Она должна изменяться при изменении соотношения сил, плотности результатов. Минимальное число матчей предлагаемой формулы должно быть таким, чтобы гарантировать участникам 100%-ную справедливость в распределении мест.

  На главную    В библиотеку    Обсудить в форуме 

При любом использовании данного материала ссылка на журнал обязательна!