|
|

ОПТИМИЗАЦИЯ БАЗЫ ПРОГНОЗА РЕЗУЛЬТАТОВ ОЛИМПИЙСКИХ ЧЕМПИОНОВ ПО ПЛАВАНИЮ В.Н. Гречанников
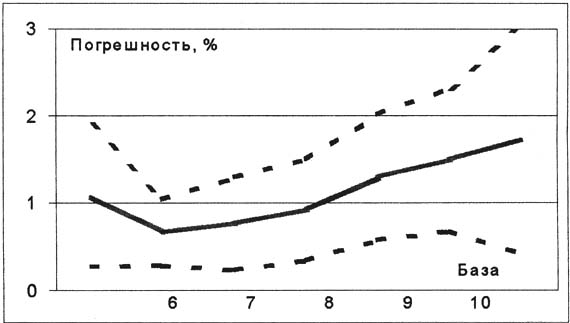
Наибольшее применение в циклических видах спорта имеют прогнозы достижений, основанные на использовании математического аппарата. Выбор наилучшей модели аппроксимации обычно осуществляется методом наименьших квадратов (МНК). Однако точность предсказания спортивных результатов не исчерпывается оптимизацией математической модели. Существенное значение имеет длина временного ряда (база). Гипотетически если ряд сравнительно невелик, то вопроса не возникает, - довольствуются тем, что имеют. Если же база включает в себя значительное число членов (в плавании это уже начинает ощущаться), то может возникнуть вопрос об оптимизации количества точек, образующих временной ряд. В противном случае точность экстраполяции, достигнутая удачным подбором модели и параметров уравнений, может в определенной степени утратиться из-за включения в расчет слишком устаревших данных. В вычислительной математике существуют подходы, связанные с применением адаптивных моделей. В них последним точкам ряда присваиваются определенные веса. Однако неизвестны критерии выбора их абсолютных величин. Следовательно, проблема определения оптимальной длины остается актуальной. Анализ доступной литературы по прогнозированию спортивных достижений свидетельствует о том, что указанная проблема в ней не обозначена. Целью работы было определить оптимальную базу в одношаговом прогнозе результатов пловцов - олимпийских чемпионов. Достижение выдвинутой цели осуществлялось методом расчетного эксперимента, содержанием которого стало проведение условно-будущего прогноза результатов чемпионов по плаванию последней Олимпиады (1996). Период наблюдения охватывал промежуток времени с 1956 по 1992 г. включитель но. В связи с изменением программы соревнований анализу подверглись результаты лишь в тех видах плавания, которые реализовались в течение всего ретроспективного периода. Таких дисциплин оказалось 11: 1500 м вольный стиль и 200 м баттерфляй, мужчины; 100 м баттерфляй, женщины; 100 м, 400 м вольный стиль, 200 м брасс, 100 м на спине, мужчины и женщины. Аппроксимация осуществлялась на компьютере с помощью системы анализа временных рядов (Версия 1.0) программной оболочки "Мезозавр", предусматривающей расчет трендов по шести моделям: линейной, квадратической, логарифмической, степенной и экспоненциальной (в двух вариантах). Расчетные величины сравнивались с фактическими результатами. Критерием оптимизации служила минимизация ошибки условного прогноза, выражаемой в процентах к теоретическим значениям. Каждый ряд описывался всеми шестью функциями. Посредством МНК выявлялся один из них для последующего анализа. Поставленная в расчетном эксперименте задача решалась в несколько этапов. На первом аппроксимация осуществлялась по максимально возможной базе (11 точек). На последующих этапах длина временного ряда в каждом виде плавания механически сокращалась за счет удаления его первого члена. С предельно короткой базой оказались ряды, состоящие из пяти точек. Дальнейшее их сокращение лимитировалось ограничениями вычислительно-процедурного характера. На рисунке представлена средняя точность условно-будущего прогноза. Видно, что погрешность экстраполяции подвержена значительным изменениям, однако укладывающимся в определенную схему. В правой части графика кривая устремляется вверх, свидетель ствуя об ухудшении точности прогноза при сравнительно длинных рядах. В средней части кривая приближается к оси абсцисс, что иллюстрирует уменьшение ошибки прогноза по мере укорочения динамических рядов. И, наконец, в крайней левой части рисунка погрешность экстраполяции вновь увеличивается. Это происходит при чрезмерном укорочении рядов.
Погрешность прогноза с различной базой временных рядов
Нельзя не заметить, что минимизация ошибки наступает тогда, когда длина временных рядов насчитывает шесть членов. Укорочение рядов или их удлинение не приводит к уменьшению погрешности прогноза. Кроме средних показателей точности экстраполяции важно обратить внимание и на их вариативность. Стандартное отклонение (полоса между штриховыми линиями на рисунке) подчиняется логике построения временного ряда, составленного из величин средней ошибки. Чем выше точность прогноза, тем меньше разброс в показателях погрешности. Всякое их отклонение от оптимальной величины приводит к росту вариабельности ошибки. По этому признаку прогноз оптимален также по шеститочечной базе. Результаты расчетного эксперимента свидетельствуют о том, что корректное привлечение обширного статистического материала, накопившегося в плавании, составляет существенный резерв в совершенствовании прогноза спортивных результатов. Для подтверждения сказанного был проведен дополнительный расчетный эксперимент: условно-будущий прогноз результатов победителей Олимпийских игр 1996 г. по всей индивидуальной части плавательной программы (24 вида) по базе из шести членов. Погрешность аппроксимации составила 0,74%. Практически такой же результат был достигнут в основном расчетном эксперименте на этапе вычислений с аналогичной базой (0,66%). Преимущества подхода становятся очевидными, если сопоставить достигнутую эффективность с ошибкой прогноза, допущенной другими авторами [1, 3, 5-8]. Их показатели варьируют в диапазоне 1,87 - 2,64%. Особняком от этих оценок стоит прогноз чемпионов по плаванию 1978 г. на московскую Олимпиаду [4]. Их ожидания оказались наиболее близки к фактическим результатам 1-1,42%. Видно, что предлагаемый в настоящей работе подход как минимум в два раза превышает эффективность предсказания других исполнителей. Это побудило к выполнению реального прогноза достижений чемпионов по плаванию на Олимпиаде-2000. Сравнение представленного прогноза с фактическими результатами делает возможным уточнить выводы, полученные в ходе расчетного эксперимента. Выводы 1. Точность прогноза спортивно-технических показателей пловцов существенно обусловлена длительностью периода наблюдения. 2. Увеличение длины временных рядов относительно оптимальной величины не приводит к повышению эффективности прогноза спортивных достижений по плаванию. 3. Оптимальная база, минимизирующая ошибку прогноза, включает шесть членов временного ряда, составленного из результатов пловцов - чемпионов Олимпийских игр. Литература 1. Абсалямов Т.М., Огородников И.А., Степанченок И.А. Принцип построения годичного цикла подготовки//Научно-спортивный вестник, 1979, № 3, с. 17-24. 2. Анохин П.К. Очерки по физиологии функциональных систем. - М.: Медицина, 1975. - 447 с. 3. Бесфорд X. Прогноз на Олимпийские игры в Москве //Информационно-методический бюллетень. - М.: ВНИИФК, отдел зарубежного спорта, 1978, № 5, с. 68-71. 4. Итоги Чемпионата мира-78 и прогнозы на Олимпиаду-80 //Спорт за рубежом. 1978, № 18, с. 8. 5. Рекордные ориентиры //Спорт за рубежом. 1978, № 12, с. 13. 6. Сколько рекордов мира падет на Олимпиаде? //Спорт за рубежом. 1976, № 1, с. 7. 7. Скорость пловцов в 1980-м //Спорт за рубежом. 1977, № 23, с. 10-11. 8. Тосунян Б. Ориентиры //Советский спорт. 10 февраля 1977. 1По известным причинам политического характера под фактическими результатами пловцов на Олимпиаде-80 принимались спортивно-технические показатели символического списка чемпионов, составленного с учетом соответствующих результатов "альтернативных" игр (г. Ирвин, США, 1980).
При любом использовании данного материала ссылка на журнал обязательна! | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Любая научно
обоснованная деятельность предполагает анализ и
предвидение ее результатов. Спортивная
деятельность направлена на достижение
максимально возможного результата индивидуума в
избранном виде двигательной активности. В силу
указанного обстоятельства она выступает в
качестве системообразующего фактора [2],
обеспечивающего эффективность
учебно-тренировочного процесса. Следовательно,
прогноз спортивно-технических показателей
является важнейшим элементом управления
учебно-тренироовочным процессом.
Любая научно
обоснованная деятельность предполагает анализ и
предвидение ее результатов. Спортивная
деятельность направлена на достижение
максимально возможного результата индивидуума в
избранном виде двигательной активности. В силу
указанного обстоятельства она выступает в
качестве системообразующего фактора [2],
обеспечивающего эффективность
учебно-тренировочного процесса. Следовательно,
прогноз спортивно-технических показателей
является важнейшим элементом управления
учебно-тренироовочным процессом.