|
|

РЕКОРД ВОЗМОЖЕН! Профессор О.В. Колодий Доцент С.С. Павлов Метание молота - это один из видов легкой атлетики, в котором состязаются самые мощные и быстрые люди планеты. Долгие годы ведущее место в данной дисциплине занимали спортсмены нашей страны. Благодаря усилиям таких спортсменов, как М. Кривоносов, Р. Клим, А. Бондарчук, А. Спиридонов, И. Никулин, Ю. Седых, С. Литвинов и др., мировой рекорд за последние тридцать лет был поднят с 65 м до 86 м 74 см. Это мировой рекорд, установленный олимпийским чемпионом Ю. Седых. В настоящее время возросла плотность результатов, обострилась борьба среди метателей молота, но только на уровне 80-83 м. Рекорд Ю. Седых, установленный в 1986 г., пока остается недосягаемым по многим причинам. В России, в которой работали несколько конкурирующих тренерских школ (киевская, минская, московская, ленинград ская и др.), умудренные опытом тренерские кадры "раздавила" перестройка, переманила "заграница", а молодежь пока не окрепла, и прежде всего из-за недостаточного финансирования. В странах, ранее конкурирующих с Россией, уровень достижений метателей молота незначительно, но вырос, что и позволяет их представителям выигрывать крупнейшие соревнования последних лет. Безусловно и то, что накопление объема специальных научных знаний наряду с отбором и подготовкой молодых талантливых спортсменов и тренеров приведет к прорыву и в спортивных результатах, но когда? Вопросы методики подготовки метателей регулярно освещались в нашей специальной литературе [1-6]. Наиболее подробно технические и методологические аспекты теории метаний самых разных снарядов (ядра, диска, копья, молота) изложены в монографии В.Н. Тутевича 1969 г. [6]. Несомненно, что данная работа стала настольной книгой для ведущих тренеров при подготовке спортсменов высокой квалификации. В монографии [6] очень обстоятельно проводится анализ влияния разных факторов (скорость и угол вылета, коэффициент лобового сопротивления движению снаряда, наличие попутного и встречного ветра и т.д.) на дальность полета молота. Результаты расчетов сведены в таблицы, в которых дается величина уменьшения дальности, обусловленная влиянием исследуемого фактора. Однако изложение физических основ самой методики, по которой проводились расчеты, в работе не приводится. Результаты расчетов, полученные с помощью предлагаемой методики, не противоречат прогнозам по дальности полета молота, которые были опубликованы в монографии В.Н. Тутевича. Различие между результатами по дальности составляет около 1,5 м, что не носит принципиального характера. В то же время любой тренер, используя разобранный пример, может оценить успехи своих учеников. С физической точки зрения метание молота - это процесс, происходящий в две стадии. Первая стадия - предварительные вращения и повороты метателя с молотом для обеспечения максимальной скорости и оптимального угла вылета снаряда. Вторая стадия происходит без участия спортсмена. Физически эта задача напоминает задачу о бросании тела под углом к горизонту. Начнем анализ проблемы с решения задачи о движении молота, брошенного метателем с начальной скоростью V0 под углом a0 к горизонту. Каковы траектория и дальность полета снаряда при известных V0 и a0 - вопросы данной задачи. Вид траектории и обозначения характерных точек и действующих сил приведены на рис.1.
Рис. 1. Уравнение движения тела ma = mg +Fсопр. Начальные условия: V(0) = VО ; a(0)=a0. Траектория движения тела под действием только силы тяжести (Fсопр = 0), брошенного под углом a0 к горизонту, представляет собой параболу, симметричную относительно вершины В. Движение по параболе есть результат суперпозиции двух движений: 1 - равномерного с постоянной скоростью (Vx (0)= V0 cosa0 ) вдоль оси ОХ; 2 - равнозамедленного до вершины В со скоростью Vy = V0sina0 - g t и равноускоренного после вершины со скоростью Vy=g( t - tB). Параметры траектории находятся с помощью следующих соотношений: - время полета до точки В tB = V0 cos a0 / g - время полета до точки С tc = 2 V0 cos a0/ g - дальность полета Xc = (V0 )2sin 2a0/ g - высота траектории УB = (V0 cos a0)2 / 2g - координата вершины XB = (V0 )2sin 2a0/ 2g. Результаты расчета дальности броска и времени полета молота представлены в табл.1. Таблица 1. Расчет кинематических величин (Fconp = 0)
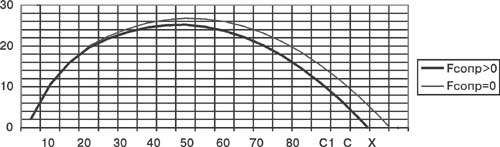
Из табл.1 видно, что для достижения максимальной дальности (Xc >85 м) в идеальном случае, без учета сопротивления воздуха, молоту необходимо сообщить скорость V0 = 29 - 30 м/с. Произведем оценку уменьшения дальности полета молота, вызванную влиянием силы сопротивления воздуха. Известно, что сила сопротивления при движении тела в воздухе определяется соотношением: Fсопр = Cx r V2 Sмид/ 2. Спортивный снаряд молот - это шар массой 7,257 кг, диаметром d>112 мм, на тросике с ручкой длиной 117-121 см. Для дальнейших расчетов примем: вес mg = 71,1 Н, диаметр d = 12 см, длина l = 120 см. Площадь миделева сечения Sмид = 1.13.10 - 2 м2. Плотность воздуха r = 1,2 кг/м3. Коэффициент лобового сопротивления Cx зависит от числа Рейнольдса Cx = f (Re). Число Рейнольдса Re = r V d / m, где m =1,01,10-3 кг/м с - коэффициент динамической вязкости воздуха. Для наших условий (V0 = 30 м/с, r = 1,2 кг/м3, d = 12 см) получаем значение числа Re " 5,3 103. Для тела в форме шара по графику Cx = f(Re) из монографии (Г. Шлихтинг "Теория пограничного слоя") находим значение Cx=0,4-0,45. Максимальное значение силы сопротивления в момент выброса молота (V0 = 30 м/с) равно Fсопр(0) = 0,4х1,2х302х1,13 х10 -2 / 2 = 2,75 Н. Заметим, что в действительности сопротивление молота из-за наличия ручки и тросика больше, чем сопротивление шара (Fсопр.мол >Fсопр.шар), и уменьшается по мере движения снаряда. Оценки показывают, что коэффициент сопротивления поводка и ручки молота на порядок меньше коэффициента сопротивления самого шара. Видим, что сила сопротивления составляет 3,8% от силы тяжести. Уравнение движения молота в проекциях на координатные оси имеет вид: m ax = - Fсопр x, где Fсопр x = Fсопр(0) cosa; m ay = - mg - Fсопр y, где Fсопр y = Fсопр(0) sina. Допустим, что составляющие силы сопротивления молота (Fсопр x , Fсопр y) остаются постоянными во время движения (допущение 1) и равными максимальным значениям силы сопротивления для шара в начальный момент времени (допущение 2). Эти два допущения оказывают противоположное действие на конечный результат, частично компенсируют друг друга и существенно облегчают решение уравнений движения. При названных допущениях движение молота вдоль оси ОХ будет равнозамедленным с ускорением ax = - Fсопр x / m; вдоль оси ОУ - равнозамедленным до вершины В1 с ускорением ay = - g - Fсопр y/m и равноускоренным после вершины В1 с ускорением ay = + g - Fсопр y/m. Это обстоятель ство позволяет целиком выполнить кинематический расчет траектории движения молота. Результаты расчета представлены ниже. Исходные данные: V(0) = 30 м /с; a(0)=45°. Данные расчетов: Vх(0) = Vу(0) = 21,2 м/с ; Fсопр x (0) = Fсопр у (0) =1,73 Н = const. Составляющие ускорения: ах = -0,24 м/с2; ау = -10,05 м/с2 (до вершины В1); ау = + 9,57 м/с2 (после вершины В1 ). Время полета до вершины В1 t(OB1) = Vу(0) /ay = 2,10 с. Координаты вершины: Хв1 =Vх(0) t(OB1 )- ах t(OB1)2/2 = 44,08 м. Ув1 = Vу(0) t(OB1) - ау t(OB1)2/2 = 22,5 м. Скорость в вершине Vх(В1) = Vх(0) - ах t(OB1) = 20,68 м / с Нисходящая ветвь траектории (участок В1С1). Как уже отмечалось выше, движение молота после вершины В1 - равноускоренное с ускорением ау = + 9,57 м/с2. Высота падения Ув1с1 = ау t(B1 С1)2/2. Отсюда время падения t(B1 С1) = 2,16 с. Общее время полета молота t(общ) = t(OB1) + t(B1 С1) = 2,10 + 2,16 = 4,26 с. Дальность нисходящей ветви траектории (рис.1): Хв1с1 = Vх(В1) t(B1 С1) - ах t(B1 С1)2/2 = 44,0 м Общая дальность: Хобщ = Хов1 + Хв1с1 = 88,08 м. Сравнивая полученные результаты для t(общ) и Хобщ с результатами расчета, приведенными в табл.1, видим, что расчетное время движения отличается от tc идеального на 0,06 с (на 1,4%), а дальность полета с учетом сопротивления воздуха меньше максимальной дальности в идеальном случае на 3,8м. Такой результат следует признать удовлетворительным, так как реальная дальность составляет 95,9% от идеального значения дальности. Проведенные расчеты показывают, что для броска молота на 87 - 88 м и более спортсмен при его разгоне во время поворотов должен сообщить ему начальную скорость вылета Vo не менее 30 м/с. Аналогичные расчеты по данной методике были проведены для начальной скорости 25, 30, 31 и 32 м/с. Результаты расчетов сведены в табл.2 и представлены на рис. 2.
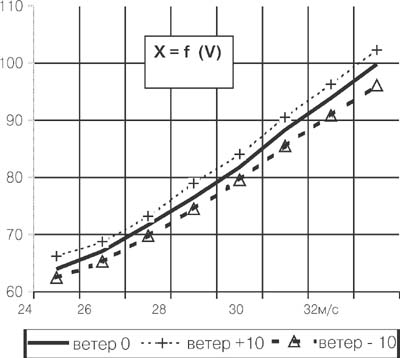
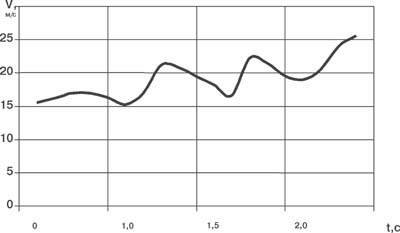
Рис. 2. Анализ расчетных данных, приведенных в табл. 2, позволяет сделать следующие выводы. Ускорение по модулю на восходящей ветви траектории всегда больше ускорения на нисходящей ее ветви. Время полета молота до вершины траектории - точки В1- меньше времени полета молота от точки В1 до точки С1. Дальность участка на восходящей ветви траектории несколько больше дальности на ее нисходящей ветви. Попутный ветер увеличивает дальность траектории, а встречный ветер - уменьшает дальность броска при одинаковой начальной скорости. Графики на рис. 2 наглядно показывают, что влияние внешних условий приводит к образованию "коридора" в значении дальности при одних и тех же параметрах выполнения броска. Это связано с изменением величины силы лобового сопротивления при изменении относительной скорости обтекания молота. Указанные выводы не противоречат физическому смыслу в рамках рассматриваемой траекторной задачи. Перейдем теперь к анализу движения молота на первой стадии [4, 5, 3, 2]. В учебнике "Легкая атлетика"[4] дан подробный анализ движений метателя молота в разных фазах. В учебно-методическом плане очень полезными можно считать кадры киносъемки вращений и поворотов с молотом ведущих метателей молота [5]. Еще более ценными представляются материалы кинематического анализа движений метателя и самого молота во время поворотов. Такой материал с анализом кинограммы броска Ю. Бакаринова на 66,7 м представлен в работе[5]. Полученный график скорости молота V = f (t) в поворотах носит принципиальный характер (рис. 3) и для разных метателей отличие будет состоять только в абсолютных значениях цифр (скорость-время) для характерных точек первой стадии броска. Заметим, что Ю. Бакаринов, не обладающий выдающимися для метателя физическими данными (рост - 169 см, вес - 100 кг), но имеющий отличные для данного времени скоростные качества и координацию движений, показывал устойчивые результаты в метании молота. Кинограммы бросков Бакаринова - наглядное пособие для тренеров и спортсменов. Анализируя кинограмму его броска, можно отметить, что в 3-м повороте приращение скорости на максимуме составляет всего 0,9 м/с, а минимальная скорость (молот находится в верхней точке) равна 18,2 м /с, т.е. чуть больше, чем при размахиваниях молотом (Vм = 17,1 м/с). И только мощное и своевременное финальное движение, когда метатель действует на молот с усилием ~ 1350 Н, позволяют сообщить снаряду приращение импульса D(mV)" 48 кгм/с, довести скорость вылета Vo до 25,6 м/с и совершить бросок за 66 м при сравнительно небольшом угле (a0=38 град) вылета молота. Если бы минимумы скорости в поворотах составляли 19, 20 и 21,5 м/с соответственно, а за счет финального усилия приращение скорости составляло 6,5 м/с, то дальность броска при той же скорости выполнения движений равнялась бы приблизительно 80 м. Но это было 30 лет назад, в настоящее время требования и класс спортсменов возросли, а это означает, что все движения в предварительных вращениях, поворотах и в финальной стадии надо делать быстрее хотя бы на 0,05 - 0,08 с. Таблица 2. Расчет кинематических величин (Fconp <> 0)
Примечание. Значок Запись 32 б/в означает, что бросок
выполнен с начальной скоростью 32 м /с в
безветренную погоду; 32 +10 - бросок с
попутным ветром 10 м/с; 32 -10 - бросок при
встречном ветре 10 м/с. Расчеты проводились при
следующих условиях: Движения молотом при размахиваниях и в поворотах должны быть с нарастающей скоростью и обеспечить ему в момент выброса наибольшую скорость Vo и оптимальный угол наклона траектории a0. Известно, что связь между линейной и угловой скоростью вращения молота определяется соотношением: V = 2pn(1 рук + 1 мол), где n - частота вращения метателя ; 1 мол - длина тросика молота (1 мол = 117,5 - 120,5 см); 1 рук - длина рук метателя (от центра масс системы до рукоятки молота) 1 рук = 55-70 см. Из приведенного соотношения следует, что для выброса молота со скоростью ~ 30 м/с и обеспечения дальности броска на 85 - 87 м метатель должен в 3-м повороте выполнить вращение со снарядом за 0,38 - 0,42 с. Это соответствует частоте вращения n = 2,4 - 2,6 об/с. С такой частотой и совершают свои движения в круге лучшие метатели молота. Почему авторы решили ликвидировать пробел в расчетах полетной стадии молота? Во-первых, всегда считалось, даже специалистами, что на дальность полета планирующих снарядов (диск и копье) сильное влияние оказывают наличие ветра и угол атаки при полете снаряда. Для снарядов с большой массой (ядро и молот) эти факторы во внимание не принимались. Однако расчеты показали, что встречный и попутный ветер необходимо учитывать и при метании молота, т.к. разница в дальности полета молота из-за влияния внешних условий может составлять 4-6 м (см. рис. 2). Во-вторых, тренерам часто приходилось сталкиваться с недоумением метателей: "Почему "не добрал" 5-6 метров? Хотя на последней тренировке все делал и чувствовал, как сегодня, а результат намного хуже". Этого не могли объяснить и тренеры. И начинались психологические срывы. Вспомните хотя бы проигрыш М. Кривоносо ва Г. Конноли на олимпиаде в Мельбурне. Исходя из этих примеров мы решили уделить большее внимание расчетам полетной стадии в метании молота и объяснению физического смысла полученных результатов.
Рис. 3. Заключение. В статье дан анализ выполнения 1-й и 2-й стадий броска метателем молота с физических позиций. Приводится методика расчета кинематических величин (дальности и времени полета) движения молота с учетом сопротивления воздуха. По данной методике произведены расчеты дальности броска для нескольких значений начальной скорости (25,30, 31 и 32 м/с). Показано влияние скорости попутного и встречного ветра на дальность полета молота. В целом это скажется на качестве прогнозирования результата и позволит тренеру вносить необходимые коррективы в тренировочный процесс при подготовке спортсменов высокого класса. Методика проведения расчетов при наличии кон-кретных данных по отдельному броску (начальная скорость и угол вылета снаряда, направление и скорость ветра) в настоящее время имеет завершенный вид. Результатами расчетов по ней могут воспользоваться отдельные тренеры или спортсмены, если обратятся на кафедру легкой атлетики ГАФК им. П.Ф. Лесгафта. Литература 1.Бондарчук А.П. Основы спортивной подготовки (метание молота). - М.: ФиС, 1985. 2. Колодий О.В., Кузнецов В.П. Динамика взаимодействия ног метателя молота с опорой: Сб. науч. тр. "Современные тенденции легкой атлетики в решении задач оздоровительной, образовательной и спортивной направленности". - М.: Госкомспорт РФ по ФК и туризму, СПбГАФК им. П.Ф.Лесгафта. СПб., 1999, с.117-120. 3. Кревальд А.А. Биомеханический анализ пространственного спортивного движения: Автореф. дис. Тарту, 1975. 4. Легкая атлетика /Под ред. О.В. Колодия, Е.М. Лутковского, В.В. Ухова. - М.: ФиС, 1985. 5. Легкая атлетика. 1962, № 2, 8; 1963, №8; 1964, № 5, 11; 1965 №5,11; 1984, № 4; 1985, № 2; 1987, №1. 6. Тутевич В.Н. Теория спортивных метаний (механико-математические основы). - М.: ФиС, 1969.
При любом использовании данного материала ссылка на журнал обязательна!
Реклама:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||