Abstract MATHEMATICAL METHODS OF DEFINITION OF CONTENTS OF SPORTS EDUCATION N.I. Sannikova, Ph. D. Nizhnevartovsk state pedagogical institute, Nizhnevartovsk Key words: education, quality, contents of education, mathematical model of contents of education, set, columns, matrix. The problems of the improvement of the quality of training of the sports staff in a higher school are considered in the article. The author has shown, that it can be achieved on the basis of the perfection of the sports education's contents. One of the ways to improve the quality of training of the sports staff offered by the author was the construction of the contents of sports education on the basis of the combination of an empirical method, exact mathematical methods, and the method of the structural analysis.
|

МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ СОДЕРЖАНИЯ ФИЗКУЛЬТУРНОГО ОБРАЗОВАНИЯ Кандидат
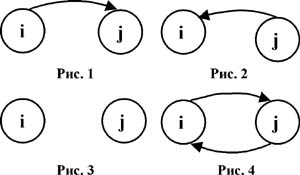
педагогических наук Н.И.Санникова Ключевые слова: образование, качество, содержание образования, математическая модель содержания образования, множество, граф, матрица. Как отметил министр образования РФ В.М. Филиппов, важнейшей задачей, стоящей перед высшим образованием в ближайшее время, является разработка и внедрение механизмов обеспечения качества образовательного процесса. С введением новых квалификационных требований все большую актуальность в настоящее время приобретают вопросы прогнозирования, перспективного планирования и оптимального управления подготовкой специалистов высшей школы, в том числе и по физической культуре. Один из главных компонентов учебного процесса в вузе - содержание образования. В последние годы проблема методологии научного обоснования содержания образования привлекает внимание все большего числа исследователей (В.С. Леднев,1991; В.А. Роменец, Н.А. Селезнева, И.Б. Моргунов, Т.В. Нерсесов,1990; В.И. Каган, И.А. Сычеников,1987, и др). Содержание образования в педагогике определяется как "совокупность систематизированных знаний, умений и навыков, взглядов и убеждений, а также как определенный уровень развития познавательных сил и практической подготовки, достигнутых в результате учебно-воспитательной работы". В качестве постулатов построения содержания образования выступают принципы научности, систематичности, связи теории с практикой, доступности. При построении содержания образования основными теоретическими подходами являются эмпирический подход, точные математические методы, метод структурного анализа. Одно из актуальных направлений совершенствования качества подготовки специалистов по физической культуре и спорту в высшей школе - построение содержания физкультурного образования на основе математических моделей. Построение математических моделей содержания образования осуществляется на основе точных математических методов - теории множеств, теории графов, теории матриц, математической статистики, теории вероятностей. Применение этого аппарата позволяет "...фиксировать разделы программ в виде множества объектов, а логические связи между ними в виде графов и матриц. Использование аппарата математической статистики позволяет получить количественные оценки значимости соответствующих разделов программы для практической деятельности специалистов". Основными единицами построения содержания образования являются учебный план, учебная программа, рабочая программа. Последние документы конкретизируются в учебниках, учебных пособиях и других учебно-методических материалах. Важная составляющая содержания образования - учебная единица, под которой понимается объем учебного материала, выраженный в единицах измерения информации - байтах. В большинстве гуманитарных курсов в качестве объема учебной единицы принимается часть текста, например 1/3 текста страницы. Количество учебных единиц должно соответствовать возможностям учебного плана. Так, если на изучение дисциплины отводится А часов учебного времени, то общее число учебных единиц не должно превышать 7А, если считать, что средний студент способен усвоить 5-7 учебных единиц в течение одного академического часа. "Учебные единицы могут иметь незначительный объем, как, например, понятие, теоремы, задачи, а могут быть и весьма емкими, как, например, раздел, дисциплина. Поэтому для удобства целесообразно рассматривать так называемые элементарные учебные единицы, охватывающие минимальный объем". Построение содержания образования, процессы создания учебных планов и учебных программ на основе математического моделирования в настоящее время ведутся в Московском институте стали и сплавов, Нижневартовском пединституте, Новосибирском педуниверситете, Омском педуниверситете и других вузах преимущественно в области математического, технического, медицинского образования. Рассмотрим вопросы построения математической модели содержания физкультурного образования. В соответствии с методикой, описанной в работах, для этого необходимо определить множество X, элементами которого являются учебные единицы (УЕ): X = {x1 ; x2 ; ... ; xn }. Затем строится граф, состоящий из элементов множества X. Логические связи в графе обозначаются дугами cо стрелками. Дуга ( хi хj ) означает, что при изучении УЕ хj в той или иной степени используется УЕ хi. Эта ситуация представлена графом на рис. 1. Обратная ситуация, в которой изучение УЕ хi опирается на УЕ хj, представлена графом на рис. 2. На рис. 3 представлен граф, в котором УЕ хi , и xj изучаются независимо друг от друга. На рис. 4 представлена петля, которая иллюстрирует противоречивую ситуацию, когда при изучении УЕ xi необходимо опираться на УЕ xj, и наоборот. На основании графа строится матрица логических связей графа, вершинами которого являются УЕ множества X = {х1 ; х2 ; ... ; хn}. Ее элемент aij ( i j ) равен 1, если изучение УЕ xi опирается на УЕ xj. Так как при изучении УЕ xi невозможно опираться на эту же УЕ, то считается по определению, что элементы матрицы логических связей с одинаковыми индексами равны нулю: аij = 0. Если изучение УЕ хi не опирается на УЕ хj, считается, что аij = 0. Затем матрица возводится в степень с целью определения наличия в графе контуров и петель. Если контуры и петли есть, то от них избавляются следующим образом: петли не изображают, а из контуров убирают какую-либо дугу, выбор которой зависит от конкретной ситуации. От контуров можно избавиться иначе, если некоторые УЕ расчленить на более мелкие подходящим образом.
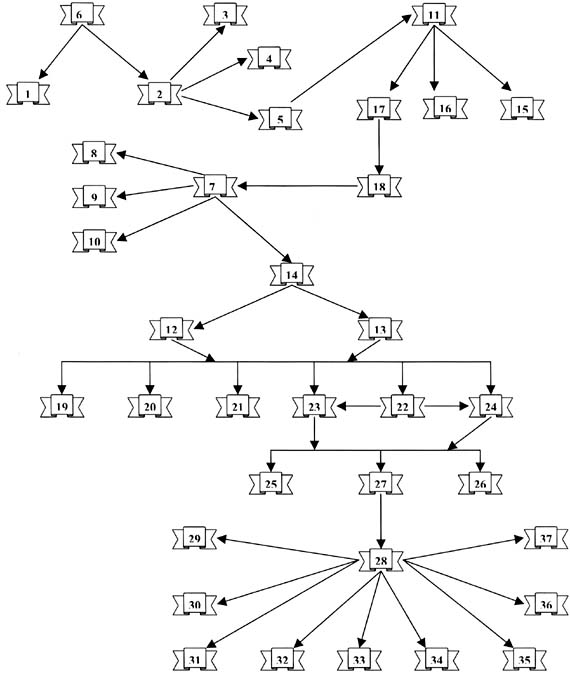
Если после возведения в некоторую степень матрица обращается в нулевую, это свидетельствует о том, что исходный граф не имеет контуров и петель. Поэтому матрицу А можно исследовать на предмет построения последовательности изучения УЕ. Последовательность изучения материала определяется следующим образом: в первую очередь изучаются УЕ, столбцы которых состоят из нулей. Для того чтобы определить, какие УЕ следует изучать во вторую очередь, в матрице А вычеркиваются УЕ, столбцы которых состоят из нулей, и строки с теми же номерами. Таким же образом определяются УЕ, которые необходимо изучать в третью, четвертую и т.д. очередь. Приведем конкретный пример. Проанализируем тему "Спортивная физиология" курса "Физиология физического воспитания и спорта" (Солодков А.С., Сологуб Е.Б. Физиология человека. Общая. Спортивная. Возрастная: Учебник. - М.: Терра-Спорт, Олимпия-Пресс, 2001, с. 177-187). Элементарные учебные единицы темы "Физиология спорта". Рассмотрим множество Х, состоящее из следующих элементов - учебных единиц: х1 - места преподавания спортивной физиологии; х2 - материалы, используемые в преподавании спортивной физиологии; х3 - основные разделы спортивной физиологии; х4 - содержание первого раздела спортивной физиологии - общей спортивной физиологии; х5 - содержание второго раздела спортивной физиологии - частной спортивной физиологии; х6 - определение понятия "спортивная физиология"; х7 - учебные и научные дисциплины, с которыми связана спортивная физиология; х8 - связь спортивной физиологии с биологией, физиологией человека и животных, химией и физикой; х9 - связь спортивной физиологии с анатомией, биохимией, биомеханикой, гигиеной и психологией; х10 - связь спортивной физиологии с теорией и методикой физической культуры, педагогикой, спортивно -педагогическими дисциплинами, спортивной медициной, лечебной физкультурой; х11 - спортивная физиология как прикладная и в основном профилактическая наука; х12 - особенности использования методик исследования в спортивной физиологии; х13 - специальные нагрузочные тесты, используемые в исследованиях по спортивной физиологии; х14 - значимость знаний по физиологии спорта для тренера и педагога; х15 - первая проблема, которую решает спортивная физиология; х16 - вторая проблема, которую решает спортивная физиология; х17 - взаимосвязь проблем, которые решает спортивная физиология; х18 - как следует изучать и оценивать физиологические особенности функций организма при спортивной деятельности; х19 - время создания института физического образования им. П.Ф. Лесгафта; х20 - первая кафедра физиологии в физкультурных вузах; х21 - заслуги Л.А. Орбели в области физиологии спорта; х22 - начальный, первый, период становления спортивной физиологии; х23 - заслуги А.Н. Крестовникова в области физиологии спорта; х24 - второй, переходный, период развития спортивной физиологии; х25 - заслуги Н.В. Зимкина в области физиологии спорта; х26 - современный, третий, период развития спортивной физиологии; х27 - ученые, занимавшиеся вопросами изучения влияния физической активности на двигательную систему; х28 - основные направления исследований по спортивной физиологии в настоящее время; х29 - приоритетные направления дальнейших исследований физиологии ЦНС при занятиях спортом; х30 - приоритетные направления дальнейших исследований по спортивной генетике; х31 - приоритетные направления дальнейших исследований по сердечно-сосудистой системе при занятиях физической культурой и спортом; х32 - приоритетные направления дальнейших исследований по дыхательной системе при занятиях физической культурой и спортом; х33 - приоритетные направления дальнейших исследований по вопросам восстановления после напряженных тренировочных и соревновательных нагрузок; х34 - приоритетные направления дальнейших исследований по специальным теоретическим вопросам при занятиях физической культурой и спортом; х35 - значимость экспресс-методов, компьютеров для проведения комплексных обследований спортсменов; х36 - приоритетные направления дальнейших исследований в области массовой физической культуры, в области физической подготовки специальных контингентов; х37 - значимость теоретических проблем и фундаментальных исследований для практики. Граф темы "Физиология спорта". Исходя из логики темы, можно построить следующий граф (рис. 5). Матрица темы "Физиология спорта". Составляем соответствующую матрицу А логических связей. При этом для удобства, чтобы сохранить нумерацию строк и столбцов, представим матрицу в виде, содержащем по дополнительному столбцу и строке с номерами (рис. 6). Для возведения матрицы в степень воспользуемся специальной компьютерной программой, разработанной в Нижневартовском государственном педагогическом институте. Возведение матрицы логических связей в 14-ю степень приводит к нулевой матрице. Это говорит о том, что граф не содержит путей длины 14 и выше, а также не содержит контуров и петель. Последовательность изучения темы "Физиология спорта". Определим порядок изучения УЕ. В первую очередь следует изучать дидактическую единицу: определение понятия "спортивная физиология". В матрице логических связей соответствующего графа вычеркиваем строки и столбцы с номером 6. Получаем матрицу 36х36. Во вторую очередь - дидактические единицы: места преподавания спортивной физиологии; материалы, используемые в преподавании спортивной физиологии. В предыдущей матрице вычеркиваем строки и столбцы с номерами 1, 2. Получаем матрицу 34х34. В третью очередь - дидактические единицы: основные разделы спортивной физиологии; содержание первого раздела спортивной физиологии - общей спортивной физиологии; содержание второго раздела спортивной физиологии - частной спортивной физиологии. В последней матрице вычеркиваем столбики и строки с номерами 3, 4, 5. Приходим к матрице 31х31. В четвертую очередь - дидактическую единицу: спортивная физиология как прикладная и в основном профилактическая наука. В последней матрице вычеркиваем столбец и строку с номером 11. Приходим к матрице 30х30.
Рис. 5. Граф темы "Физиология спорта" В пятую очередь - дидактические единицы: первая проблема, которую решает спортивная физиология; вторая проблема, которую решает спортивная физиология; взаимосвязь проблем, которые решает спортивная физиология. В последней матрице вычеркиваем столбец и строку с номерами 15, 16, 17. Приходим к матрице 27х27. В шестую очередь - дидактическую единицу: как следует изучать и оценивать физиологические особенности функций организма при спортивной деятельности. В последней матрице вычеркиваем столбец и строку с номером 18. Приходим к матрице 26х26. В седьмую очередь - учебные и научные дисциплины, с которыми связана спортивная физиология. В последней матрице вычеркиваем столбец и строку с номером 7. Приходим к матрице 25х25. В восьмую очередь - следующие дидактические единицы в любой последовательности: связь спортивной физиологии с биологией, физиологией человека и животных, химией и физикой; связь спортивной физиологии с анатомией, биохимией, биомеханикой, гигиеной и психологией. В последней матрице вычеркиваем столбцы и строки с номерами 8, 9, 10, 14. Приходим к матрице 21х21. В девятую очередь - особенности использования методик исследования в спортивной физиологии; специальные нагрузочные тесты, используемые в исследованиях по спортивной физиологии. В последней матрице вычеркиваем столбцы и строки с номерами 12,13. Приходим к матрице 19х19. В десятую очередь - следующие дидактические единицы: время создания института физического образования им. П.Ф. Лесгафта; первая кафедра физиологии в физкультурных вузах; заслуги Л.А. Орбели в области физиологии спорта; начальный, первый, период становления спортивной физиологии. В последней матрице вычеркиваем столбцы и строки с номерами 19, 20, 21, 22. Приходим к матрице 15х15. В одиннадцатую очередь - заслуги А.Н. Крестовникова в области физиологии спорта; второй, переходный, период развития спортивной физиологии. В последней матрице вычеркиваем столбцы и строки с номерами 23, 24. Приходим к матрице 13х13. В двенадцатую очередь - заслуги Н.В.Зимкина в области физиологии спорта; современный, третий, период развития спортивной физиологии; ученые, занимавшиеся вопросами изучения влияния физической активности на двигательную систему. В последней матрице вычеркиваем столбцы и строки с номерами 25, 26, 27. Приходим к матрице 10х10. В тринадцатую очередь - основные направления исследований по спортивной физиологии в настоящее время. В последней матрице вычеркиваем столбец и строку с номером 28. Приходим к матрице 9х9. В четырнадцатую, последнюю,
очередь - следующие дидактические
единицы в любой
последовательности: приоритетные
направления дальнейших
исследований физиологии ЦНС
при занятиях спортом, приоритетные
направления дальнейших
исследований по спортивной
генетике; приоритетные направления
дальнейших исследований по сердечно
-сосудистой системе при занятиях
физической культурой и спортом;
приоритетные направления
дальнейших исследований по дыхательной
системе при занятиях физической
культурой и спортом; приоритетные
направления дальнейших
исследований по вопросам
восстановления после напряженных
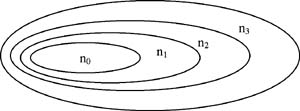
тренировочных и В последней матрице вычеркиваем столбцы и строки с номерами 29, 30, 31, 32, 33, 34, 35, 36, 37. Приходим к нулевой матрице. На основании проведенного анализа можно определить следующую последовательность изучения основных разделов темы "Физиология спорта": 1. Спортивная физиология как учебная и научная дисциплина: 1) 6; 2) 1, 2; 3) 3, 4, 5; 4) 11; 5) 15, 16, 17; 6) 18. 2. Связь спортивной физиологии с другими учебными и научными дисциплинами: 1) 7; 2) 8, 9, 10, 14. 3. Методики исследований в спортивной физиологии: 1) 12, 13. 4. История развития спортивной физиологии: 1) первый период - 19, 20, 21, 22; 2) второй период - 23, 24; 3) третий, современный, период - 25, 26, 27. 5. Состояние и перспективы развития спортивной физиологии: 1) направления исследований - 28; 2) основные направления исследований в настоящее время - 29, 30, 31, 32, 33, 34, 35, 36, 37. Порядок изучения дидактических единиц для наглядности можно графически представить в виде последовательности концентрических овалов следующим образом. В центральном круге располагаются те единицы, которые следует изучать в первую очередь; в кольце между центральным кругом и последующим располагаются единицы, которые следует изучать во вторую очередь, и т.д. На рис. 7 представлен общий случай, где указано количество дидактических единиц.
Рис. 6. Матрица темы "Физиология спорта" Для нашего примера характерна такая последовательность концентрических кругов (рис. 8). При структурировании учебного материала, содержащего небольшое количество дидактических единиц, можно применять метод структурного анализа, который представляет собой "ослабленный" вариант рассмотренного выше точного математического метода. Структурный анализ дидактической единицы проводится в два этапа. Первый этап - это нисходящий анализ, при котором выделяются дидактические единицы, приводящие к данной дидактической единице. Второй этап - восходящий анализ, при котором выделяются производные от данной дидактической единицы. Как правило, на втором этапе устанавливаются связи между производными дидактическими единицами. На практике результаты структурного анализа удобно иллюстрировать в виде "дерева", которое является частным случаем графа. Заключение. При сравнительном анализе полученных результатов с исходными данными можно отметить некоторое несовпадение в последовательности изложения дидактических единиц, выделенных по учебнику, с тем, которое получилось после математического анализа. Это дает основание считать, что использование точных математических методов позволяет упорядочить изложение содержания учебного материала. В то же время знание количества и очередности дидактических единиц позволит более обоснованно распределять учебный материал от занятия к занятию по этапам многоступенчатой (общеобразовательная школа - среднее профессиональное образование - высшее профессиональное образование ) или многоуровневой (специалист - бакалавр - магистр) подготовки физкультурных кадров. Кроме того, знание содержания дидактических единиц позволит более целенаправленно выстраивать межпредметные связи по учебным дисциплинам. Таким образом: одним из путей повышения качества подготовки физкультурных кадров является построение содержания физкультурного образования на основе сочетания эмпирического метода, точных математических методов, метода структурного анализа.
Рис. 7
Рис. 8
При любом использовании данного материала ссылка на журнал обязательна! |