Abstract ACCURACY OF MOTOR ACTIONS AT INTERACTION WITH POWER OF A VARIOUS NATURE O.B. Nemtsev, Ph. D. Institute of physical culture and judo of Adygej state university, Maikop Key words: accuracy of movement, central and peripheral factors. The author studied dynamics of kinematic structure of the maximum fast exact movements with the amplitude 10 and 20 sm. 58 girls took part in the experiment. In each task the average arithmetic of ten attempts was taken into account. The researches were carried out on the device developed and made in the laboratory of biomechanics of the Adygej state university. It was offered to the examinee to execute The movement by a hand upwards- downwards as soon as possible, touching with the probe, connected with the analog-digital converter by a wire, a high-resistance string on which the voltage 0,1 V is sent.
|

ТОЧНОСТЬ ДВИЖЕНИЙ ПРИ ВЗАИМОДЕЙСТВИИ С СИЛАМИ РАЗЛИЧНОЙ ПРИРОДЫ Кандидат
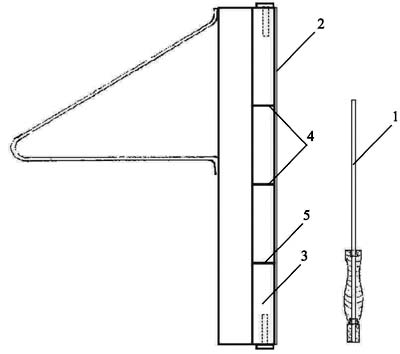
педагогических наук О.Б. Немцев Ключевые слова: точность движения, центральные и периферические факторы. В спорте существует широкий круг двигательных действий, эффективность которых зависит от способности проявлять высокую точность одновременно с силой и быстротой. В ряде предшествующих исследований отмечено снижение точности движений (как одного из критериев техники) во время реализации "блоков" интенсивной силовой подготовки [1] после непосредственно предшествующей нагрузки силового характера [3, 4], а также в результате силовой подготовки, не сочетающейся с развитием точности [6]. Это делает актуальной проблему интеграции скоростно-силовой подготовки и процесса развития точности. Очевидно, что выполнение упражнений скоростно-силовой направленности может отрицательно сказываться на уровне точности вследствие воздействия на центральные и периферические механизмы организации точностных двигательных действий. Так, например, импульсация проприорецепторов, свидетельствующая о выполнении движений при приобретении баскетбольным мячом требуемой скорости вылета, значительно отличается от той, которая необходима для коррекции положения мяча, что при выполнении только упражнений, требующих значительного проявления силы, может вызвать ухудшение способности центральной нервной системы дифференцировать слабые раздражения. Однако острота этой проблемы значительно снижается в результате сочетания скоростно-силовых и точностных упражнений в микро- и мезоциклах в зависимости от интенсивности силовой подготовки [1, 6]. В результате силовой подготовки на периферии увеличиваются мышечная масса и упругость мышц [2, 8, 7 и др.]. Бен Саид Нуреддин и Голомазов С.В. [1] установили, что между величиной электромеханического интервала (по предположению авторов, зависящей от "эластичности мышц") и точностью существует взаимосвязь. Обнаруженная взаимосвязь может быть обусловлена и следствием совершенствования центральных механизмов управления движениями в ходе силовой подготовки, в результате которой эластичность меняется c приобретением различного двигательного опыта, а вопрос о влиянии на точность движений изменения массы рабочих сегментов и упругости мышц во многом остается открытым. Попытки дать ответ на этот вопрос представлены в настоящей статье. Для сглаживания влияния реальной силовой подготовки на центральную нервную систему изменение массы и упругости мышц моделировалось при помощи увеличения отягощения грузами специального щупа, которым производилось движение (что имитировало увеличение массы рабочего сегмента руки), и присоединения к нему упругих элементов. Следует отметить, что упругие элементы крепились к щупу так, что сопротивление оказывалось при движении к цели. Таким образом имитировалось увеличение упругости антагониста в движении к цели, в нашем случае - в движении сгибание-разгибание предплечья - трицепса. Изучалась динамика кинематической структуры максимально быстрых точностных движений с амплитудой 10 и 20 см. Исследования проводились на устройстве 1, разработанном и изготовленном в лаборатории биомеханики ИФК и дзюдо АГУ (рис. 1). Испытуемому предлагалось как можно быстрее выполнить движение рукой вверх-вниз, касаясь щупом 1 (см. рис. 1), соединенным проводом с аналого-цифровым преобразователем, высокоомной нити 2, на которую подано напряжение 0,1 V, укрепленной на основании 3. При этом разворот необходимо было выполнить как можно ближе к целевой отметке (4), укрепляемой на расстоянии 10 или 20 см от стартовой отметки (5), чем задавался точностный характер движения. Программное обеспечение 2 позволяло измерять координату точки соприкосновения щупа и высокоомной нити, анализировать изменение координаты и ее производных. В эксперименте приняли участие 58 девушек (средний возраст - 19,0±0,91). В каждом задании учитывалось среднее арифметическое десяти попыток.
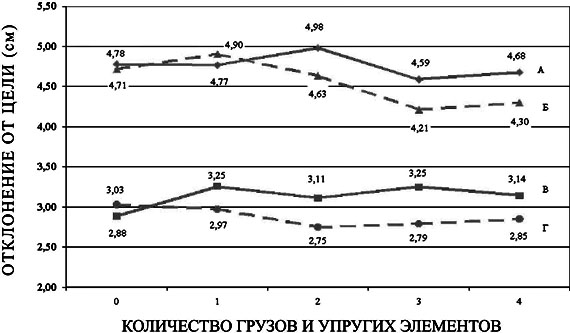
Рис. 1. Схема устройства для определения кинематических характеристик максимально быстрых точностных движений (пояснения в тексте) Из рис. 2 видно, что увеличение массы щупа в исследовавшихся пределах и числа упругих элементов привело лишь к незначительному изменению точности при движении на 10 см (p>0,053, F=0,38 при изменении массы щупа и F=0,92 при изменении числа упругих элементов, F критич.=2,40) и 20 см (p>0,05, F=0,21 при изменении массы щупа и 1,72 при изменении числа упругих элементов, F критич.=2,40). Показатели точности движений (обратно пропорциональные величине отклонения от цели) с одинаковой амплитудой при увеличении числа упругих элементов в большинстве случаев выше, чем при повышении массы щупа, однако достоверны только различия показателей точности в движениях на 20 см с 3 упругими элементами и 3 грузами (p<0,05, F=4,02, F критич.=3,92). Для выявления причин стабильности точности максимально быстрых движений со средней и большой амплитудой при противодействии сил различной природы рассмотрим динамику других кинематических параметров в зависимости от изменения массы щупа и количества упругих элементов. В движениях на 10 см увеличение массы щупа или количества упругих элементов (силы упругого сопротивления) не оказывает значительного изменения большинства исследуемых показателей. При увеличении массы щупа происходят лишь разновеликие и часто разнонаправленные изменения времени достижения максимума скорости в движении к цели (Tmax v), времени от достижения цели до достижения максимума перемещения (max S), от достижения max S до обратного достижения цели и последующего движения до обратного достижения старта. Это подтверждает их случайность. Прослеживается тенденция к некоторому уменьшению времени движения к цели и времени всего движения, а также увеличению максимальной скорости в движении к цели (max v), но все различия недостоверны (p>0,05). С увеличением силы упругого сопротивления движению к цели достоверно уменьшается лишь Tmax v (p<0,01, F=3,61, F критич.=3,39). Обратим также внимание на разнонаправленное изменение времени движения к цели (уменьшение) и обратного движения (увеличение) при некотором росте максимальной скорости движения к цели. Различия указанных параметров при увеличении силы упругого сопротивления не достигают достоверных величин (p>0,05), однако эта тенденция полностью повторяется в движениях с амплитудой 20 см, где различия уже достоверны (p<0,001, F=6,97 для показателей времени движения к цели и 5,19 - для показателей max v, F критич.=4,75, p<0,05, F=3,25, F критич.=2,40 - для показателей времени обратного движения). То есть, совершая при увеличении силы упругого сопротивления движение к цели значительно быстрее, не теряя скорости на развороте (различия времени цель - max S, max S - обратное достижение цели при изменении силы упругого сопротивления недостоверны - p>0,05, F=0,84 и 1,28 соответственно, F критич.=2,40), испытуемые значительно увеличивали время обратного движения, что не позволяло им уменьшить время всего максимально быстрого точностного движения. Очевидно, возрастающая внешняя сила упругости все более замещает функцию мышц-антагонистов, способствует развитию большего напряжения агонистов до начала движения, что позволяет быстрее (различия Tmax v достоверны, p<0,01, F=3,41, F критич.=3,39) развивать большую max v (p<0,001, F=5,96, F критич.=4,75), но не способствует своевременному, опережающему включению антагонистов в работу, в результате чего увеличивается время обратного движения. Увеличивающаяся масса щупа в движениях на 20 см также способствует развитию напряжения агонистов до начала движения, и это тоже дает возможность быстрее (p<0,05, F=2,74, F критич.=2,40) развить большую скорость (p<0,05, F=2,86, F критич.=2,40) и уменьшить время движения к цели (p<0,01, F=5,71, F критич.=3,39). Однако затем в отличие от движений с сопротивлением силы упругости не происходит снижения эффективности работы пары агонист-антагонист. Также, очевидно, более раннее включение антагониста позволяет накопить больше энергии, что приводит к некоторому уменьшению времени от достижения max S до обратного достижения цели (хотя различия не достоверны, p>0,05, F=0,81, F критич.=2,40), не увеличивать время обратного движения после сопротивления увеличившейся силе инерции (p>0,05, F=0,75, F критич.=2,40) и выполнять все реверсивное точностное движение гораздо быстрее (p<0,05, F=3,30, F критич.=2,40).
Рис. 2. Точность максимально быстрых точностных движений при воздействии сил различной природы: А - 10 см F тяж., Б - 10 см F упруг., В - 20 см F тяж., Г - 20 см F упруг. Точность движений на 20 см во всех случаях намного выше, чем на 10 см (p<0,001). Причем следует отметить, что точность растет пропорционально длительности движения к цели, а не амплитуды реверсивного точностного движения и вопреки росту максимальной скорости. Это подтверждает вывод о ведущем значении для сложности программирования максимально быстрого точностного движения именно его времени, изменение которого увеличивает или уменьшает степень последовательности актуализации элементарных двигательных программ [5]. Анализ данных эксперимента позволяет заключить, что даже при значительном влиянии внешних сил на биомеханическую структуру максимально быстрого точностного движения, существенной трансформации взаимосвязей между еe элементами, выразившихся в достоверных изменениях временных и пространственно-временных характеристик движений, результат движений как механической части точностных двигательных действий, их точность оказались стабильными. Данные о стабильности точности при изменении внешних сил тяжести и упругости и ее возможной динамике и их причинах не только согласуются с выводами [9] о том, что движения программируются в строгом соответствии с инерционными характеристиками сегментов тела, но и показывают механизмы достижения такого соответствия. Полученные результаты позволяют сделать два основных вывода, значимых для теории и практики физического воспитания и спорта. Во-первых, разнонаправленная динамика точности при увеличении массы щупа и числа упругих элементов, противодействующих движению к цели, дает основание считать увеличение массы рабочих сегментов тела, участвующих в точностном движении, отрицательным, а увеличение упругости рабочих мышц - положительными периферическими факторами в достижении точности. Это, в свою очередь, определяет выбор методов силовой подготовки при повышении эффективности двигательных действий, требующих значительного проявления точности и силы. Во-вторых, изменение инерционных характеристик щупа (и предположительно сегментов тела) и силы упругости, препятствующей движению (упругости антагониста), оказывают воздействие на центральный аппарат управления, который в целом успешно справляется с новой биомеханической ситуацией. Так как в результате применения большинства методов развития силы в той или иной мере возрастает и масса мышц, и их упругость, то эти два фактора влияют на точность движений и в значительной мере компенсируют друг друга. Литература 1. Бен Саид Нуреддин, Голомазов С.В. Индивидуальные особенности проявления электромеханического интервала и точность двигательных действий // Юбилейный сборник трудов ученых РГАФК, посвященный 80-летию академии. Т. 1. - М.: ФОН, 1997, с. 65-69. 2. Верхошанский Ю.В. Программирование и организация тренировочного процесса. - М.: ФиС, 1985. - 176 с. 3. Воробьёв А.Н. Тяжелоатлетический спорт. Очерки по физиологии и спортивной тренировке. - М.: ФиС, 1977, с. 46-48. 4. Голомазов С.В. Теоретические основы и методика совершенствования целевой точности двигательных действий: Докт. дис. М., 1996, с. 176. 5. Доронин А.М., Немцев О.Б., Поляков С.В. Влияние силовой нагрузки на временную структуру движений // Актуальные проблемы валеологии, воспитания учащихся в условиях новой концепции физкультурного образования: Материалы. междунар. науч. конф. - Нальчик: Изд-во КабБГУ, 2002, с. 167-168. 6. Немцев О.Б. Основы точности как физического качества человека: Учеб. пос. - Майкоп: Изд-во АГУ, 2003, с. 4-9. 7. Немцев О.Б. Формирование точности движений средствами и методами физического воспитания у юношей и девушек 15-17 лет (на примере операторов ПЭВМ): Автореф. канд . дис. Майкоп, 1999. - 23 с. 8. Уилмор Дж.Х., Костилл Д.Л. Физиология спорта. - Киев: Олимпийская литература, 2001, с. 63-70. 9. Энока Р.М. Основы кинезиологии. - Киев: Олимпийская литература, 2000, с. 304-306. 10. Collyer C.E., Broadbent H.A., Church R.M. Preferred rates of repetitive tapping and categorical time production // Perception and Psychophysics. - 1994. - V. 55. - P. 443-453. 1 Рационализаторское предложение, принятое в АГУ, № 40-05 от 12 июля 2002 г. Авторы: О.Б. Немцев, А.М. Доронин, С.В. Поляков. 2 Разработано инженером-программистом лаборатории биомеханики ИФК и дзюдо АГУ С.В. Поляковым по алгоритмам автора. 3 Достоверность различий определялась при помощи однофакторного дисперсионного анализа (ANOVA).
При любом использовании данного материала ссылка на журнал обязательна! |