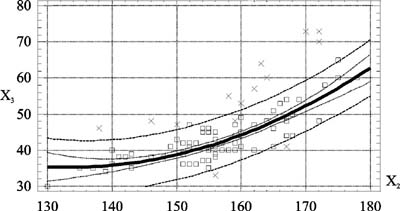
Ключевые слова: физическое развитие, моделирование, прогнозирование, гармоничность, должные нормы.

Физическое воспитание детей, подростков и юношей осуществляется в конкретной окружающей среде, факторами которой являются как социально -экономические, так и экологические условия. Поэтому физическое состояние детей, с одной стороны, можно рассматривать как результат влияния этих условий, а при направленном воздействии физического воспитания - как результат противодействия негативным условиям окружающей среды.

Физическое воспитание - неотъемлемая составляющая системы образования детей, подростков и юношей (молодежи), способствующая формированию всесторонне духовно и физически развитого человека и обеспечивающая его безопасную жизнедеятельность.

Кроме того, цель физического воспитания - удовлетворение потребностей человека в двигательной активности, достижение такого уровня физического состояния, которое обеспечивает полноценное физическое здоровье.

По поводу трактовки терминов "здоровье" и "физическое здоровье" существует много мнений. Однако понятие "физическое состояние" более близко нашему пониманию и имеет достаточно четкие критерии определения.

Согласно определению Международного комитета по стандартизации тестов, физическое состояние характеризует личность человека, состояние здоровья, телосложение, конституцию, функциональные возможности организма, физическую работоспособность.

Таким образом, для практического использования в физическом воспитании мы можем выбрать доступные и информативные показатели физического состояния, которые можно измерить и оценить. Это могут быть: соматометрические, соматоскопические и физиометрические показатели, физическая подготовленность, двигательная активность, заболеваемость.

При выборе измеряемых признаков физического состояния необходимо учитывать простоту их измерения, способы оценки и мотивацию занимающихся.

При оценке антропометрических признаков физического развития используют в большинстве случаев антропометрические стандарты для конкретных возрастных групп. При оценке нескольких признаков возникает необходимость сопоставить уровень каждого, а затем их совпадение или несовпадение, чтобы определить гармоничность или дисгармоничность развития [1, 3, 6]. Такой оценке в основном подвергаются параметры длины, массы тела и окружности грудной клетки. Гармоничность телосложения мальчиков и девочек определяется не ранее юношеского возраста, когда заканчивается половое созревание и появляется возможность использования силовой тренировки с целью коррекции фигуры [4, 5, 8]. В доступной нам литературе мы не встречали математических моделей определения величин обхватных и длиннотных показателей, характерных для подростков 13-15 лет в период пубертатного скачка. Измерение данных показателей соответствует мотивам и интересам подростков (и юношей и девушек) в их стремлении к внешней красоте и ориентирует их на достижение гармонии телосложения, во многих случаях предостерегая от чрезмерного худения девушек и гипертрофии в развитии отдельных мышечных групп - юношей, и в то же время является стимулом к занятиям физическими упражнениями. Методы факторного и регрессионного анализов [7] позволили выделить антропометрические признаки, наиболее тесно связанные между собой, и разработать математические модели определения обхватных и линейно-весовых показателей, характерных для подростков 13-15 лет.

Процедура факторного анализа сформировала систему факторных нагрузок. На первый фактор пришлось 25,6% общей дисперсии, и он был верифицирован как "физическое развитие". В него вошли следующие показатели:

Х₂ - длина тела (см); Х₃ - масса тела (кг); Х₄ - обхват грудной клетки в покое (см); Х₅ - обхват грудной клетки на вдохе (см); Х₆ - обхват грудной клетки на выдохе (см); Х₇ - экскурсия грудной клетки (см); Х₈ - обхват плеча (см); Х₉ - обхват бедра (см); Х₁₀ - обхват талии (см).

Принципиальной задачей анализа набора переменных в пределах выделенного фактора являлось установление базовых показателей, используя которые можно построить математические модели для прогнозирования с достаточной для практики степенью точности значения остальных производных от базовых переменных. Решение этой задачи позволит:

- исключить производные переменные из исходного набора переменных;

- упростить модель структуры факторного пространства;

- рационально перераспределить дисперсию между базовыми и остальными переменными, используя метод главных компонент;

- легко интерпретировать содержание выделенных факторов.

Задача выбора базовых переменных была решена методом кластерного анализа линейно-весовых показателей физического равития. Метод кластеризации - k-средние, метрика пространства - евклидово расстояние. Процедура кластерного анализа завершилась формированием границ трех непересекающихся кластеров из контингента школьников, четко различающихся по длине тела и массе. В таблице приводятся данные об абсолютном и относительном содержании каждого кластера и координатах выделенных кластеров на плоскости Х₂ - Х₃.

Большинство школьников (60,9%) оказались сосредоточенными в кластере 1, координаты которого близки к средним значениям длины тела (Х₂) и массы тела (Х₃) всей выборки, равным соответственно 156,8 см и 44,9 кг. Координаты кластера 2 (16,9% выборки) характеризуют школьников как низкорослых, масса тела которых лишь незначительно уступает массе школьников кластера 1. В кластере3, включающем 22% выборки, оказались высокорослые школьники с массой тела, на 13 кг превосходящей среднюю в выборке.

В контексте результатов кластерного анализа полезно рассмотреть зависимость между базовыми переменными - массы тела (Х₃) от его длины (Х₂). На рис. 1 приведены поле корреляции и линия регрессии. Зависимость имеет явно нелинейный характер. Ее главными особенностями являются наличие двух отличающихся областей:

- в диапазоне длины тела 130< Х₂ <150 см масса тела практически не изменяется, оставаясь в пределах значений 35...38 кг;

- в диапазоне длины тела 150< Х₂ <180 см масса тела быстро нарастает со средней скоростью 1 кг / см.

Содержание кластеров на плоскости длина тела (X₂) масса тела (X₃)

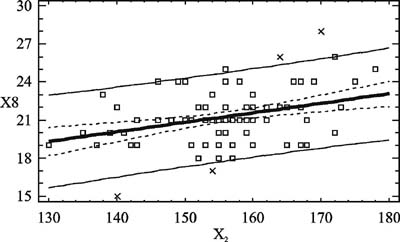
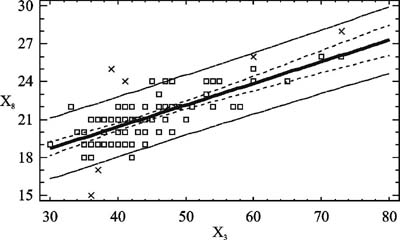
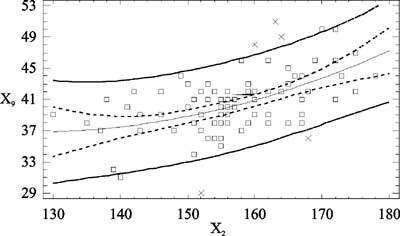
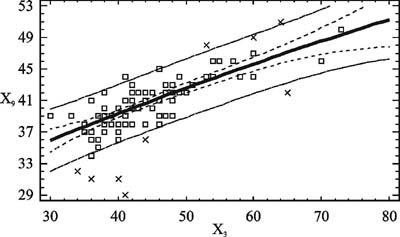
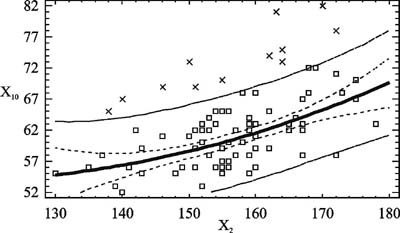
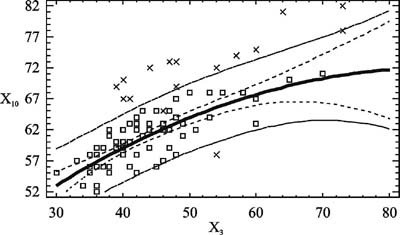
Интенсивные темпы прироста массы тела вместе с длиной тела начиная со 150 см свидетельствуют о наступлении периода интенсивного полового созревания.

Характерным является то, что такое распределение произошло в группе мальчиков одного хронологического возраста - 13 лет (всего 87 испытуемых), что свидетельствует о неоднородности группы по биологическому возрасту и возможности использования показателей длины и массы тела в качестве характеристик темпов физического развития, что подтверждает данные исследователей [2 - 7 и др.].

Поэтому мы можем использовать базовые антропометрические характеристики как основу для создания прогнозных моделей физического развития школьника.

Если такие модели будут обладать приемлемой для практики прогностической способностью, то длина тела и его масса могут быть использованы в дальнейшем для прогнозирования уровня физической работоспособности подростков вследствие возрастной однородности исследуемого контингента школьников.

Синтез прогнозной модели обхвата плеча (Х₈). На рис. 2, 3 в качестве иллюстрации приведены зависимости обхвата плеча мальчиков от длины и массы тела соответственно.

Каждая из этих зависимостей характеризуется низким коэффициентом детерминации R-кв. Синтезируя прогнозную модель, мы включили линейно в качестве регрессоров обе базовые переменные и их произведение, отражающие эффект их взаимодействия.

Результатом синтеза является прогнозное уравнение вида:

Х₈ = 0,0598·Х₂ + 0,7133·Х₃ - 0,00289·Х₂·Х₃ , см. (1)

При коэффициенте детерминации R-кв.= 99,5%, средней абсолютной ошибке 1,16 см и диапазоне изменения переменной 17 см приведенная ошибка модели составляет 6,8%. Эти данные позволяют сделать заключение, что уравнение (1) вполне пригодно для практического использования при определении гармоничности физического развития подростков-мальчиков.

Синтез прогнозной модели обхвата бедра (х₉). На рис. 4 и 5 в качестве иллюстрации приведены зависимости обхвата бедра от длины и массы тела соответственно, откуда следует, что эти зависимости достаточно близки к линейным в области действующих значений переменных.

Поступив так же, как и в предшествующем случае, получим прогнозную модель вида:

Х₉ = 0,1453·Х₂ + 1,0155·Х₃ - 0,0039·Х₂·Х₃ , см. (2)

Ее прогностические свойства достаточно высоки: коэффициент детерминации модели R-кв. = 99,6%, стандартная ошибка оценки = 2,62. При средней абсолютной ошибке = 1,89 см и диапазоне изменения объема бедра 22 см приведенная ошибка составляет не более 8,6%, что является вполне пригодным для практических целей.

Прогнозная модель обхвата талии (Х₁₀).

Обхват талии - важная переменная, косвенно характеризующая степень отложения жира, тип телосложения.

На рис. 6 и 7 представлены графики зависимостей обхвата талии мальчиков от длины тела Х₂ и массы тела Х₃ соответственно. Каждая из них обнаруживает нелинейный характер, проявляющийся по-разному.

В рассматриваемых диапазонах значений переменных увеличение длины тела сверх 150 см сопровождается быстрым возрастанием значений объема талии. Средняя крутизна этой зависимости на восходящем участке графика составляет 0,4 кг/см.

Относительно зависимости обхвата талии от массы тела можно заключить, что на начальном участке кривой (в диапазоне значений массы 30< Х₃ <45 кг) средняя крутизна составляет 0,6 см/кг. Начиная со значений массы 45 кг и более происходит замедление возрастания обхвата талии, которое у данного контингента школьников имеет предел, равный 72 см при массе тела 80 кг. Данная зависимость свидетельствует о том, что чем меньше длина тела испытуемых и больше их масса, тем больше увеличивается размер талии. Подростки ниже 150 см в 13 лет и имеющие массу тела, превышающую норму, проявляют признаки ожирения, что сказывается на обхвате их талии. При интенсивном росте тела в длину прирост массы тела замедляется, снижаются относительная масса тела и жировая прослойка (период вытягивания), что приводит к меньшему увеличению обхватных размеров талии. При замедлении темпов роста тела в длину увеличивается прирост массы тела, в том числе и размер талии. Таким образом, отличие фактического значения талии от прогнозируемого в сторону увеличения свыше 3 см в возрасте 13-15 лет может свидетельствовать об ожирении.

Учитывая описанные особенности зависимостей, были приняты в качестве кандидатов в регрессоры прогнозной модели переменные Х₂, Х₃, их квадраты Х₂·Х₂, Х₃·Х₃ и произведение Х₂·Х₃.

Рассмотрев результаты, полученные при синтезе прогнозной модели, и диапазон изменения объема талии 30 см, выводим уравнение:

Х₁₀ = 0,0012·Х₂·Х₂ + 2,5543·Х₃ - 0,0117·Х₂·Х₃ , см (3)

в качестве прогнозного, имеющего приведенную погрешность 10%.

Рис. 1. Зависимость массы тела (Х₃) школьника в диапазоне13-15 лет от длины его тела (Х₂)

Рис. 2. Зависимость обхвата плеча (Х₈) от длины тела (Х₂)

Рис. 3. Зависимость обхвата плеча (Х₈) от массы тела (Х₃)

Рис. 4. Зависимость обхвата бедра (Х₉) от длины тела (Х₂)

Рис. 5. Зависимость обхвата бедра (Х₉) от массы тела (Х₃)

Рис. 6. Зависимость обхвата талии (Х₁₀) от длины тела (Х₂)

Рис. 7. Зависимость обхвата талии (Х₁₀) от массы тела (Х₃)

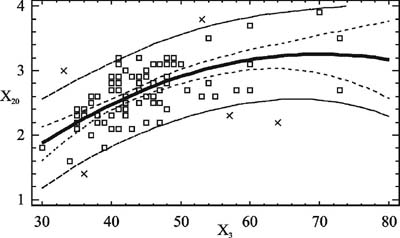
Рис. 8. Зависимость ЖЕЛ (Х₂₀) от длины тела (Х₂)

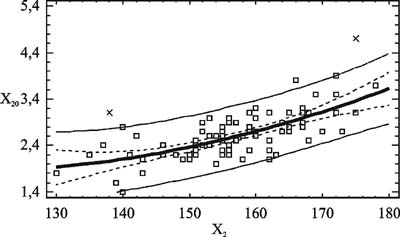
Рис. 9. Зависимость жизненной емкости легких (Х₂₀) от массы тела (Х₃)

Определение должной величины жизненной емкости легких. Жизненная емкость легких (ЖЕЛ) (Х₂₀) зависит от длины тела (Х₂) и массы тела (Х₃). Поля корреляций и частные зависимости для данного контингента школьников представлены на рис. 8 и 9 соответственно. Характер зависимостей имеет особенности, подобные графикам для обхвата талии. Обращаясь к рис. 9, можно отметить, что ЖЕЛ достигает максимального значения при массе тела, равной 70 кг.

Как и при прогнозировании обхвата талии, мы приняли в качестве кандидатов в регрессоры прогнозной модели переменные Х₂, Х₃, их квадраты Х₂·Х₂, Х₃·Х₃ и произведение Х₂·Х₃.

Результатом синтеза является уравнение для определения должной ЖЕЛ (ДЖЕЛ):

Х₂₀ = 0,0006372·Х₂·Х₃ - 0,0008964·Х₃·Х₃ , (4)

где: Х₂ - длина тела, см;

Х₃ - масса тела, кг.

После расчета ДЖЕЛ эту величину сравнивают с фактической ЖЕЛ (ФЖЕЛ) . Для этого

ФЖЕЛ
-----------  · 100
ДЖЕЛ

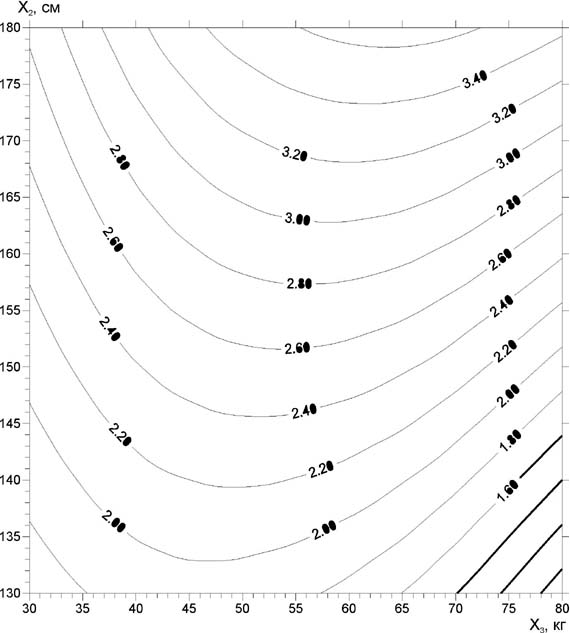
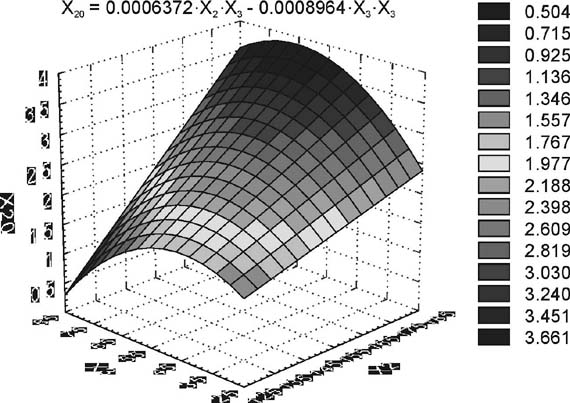
Если ФЖЕЛ меньше ДЖЕЛ более чем на 10-15%, это свидетельствует о сниженной функции внешнего дыхания, а если превышает ДЖЕЛ, то указывает на высокое функциональное состояние легких.

Прогностические свойства модели достаточно высоки: коэффициент детерминации R-кв.= 98,1%, стандартная ошибка оценки = 0,37 л. При средней абсолютной ошибке в 0,28 л и диапазоне изменения ЖЕЛ в 3,3 л приведенная ошибка составляет не более 8,5%, что вполне приемлемо для практических целей.

На плоскости Х₃ - Х₂ (рис 10) построены линии постоянного уровня ЖЕЛ. Рассматривая эти линии, можно заметить, что главное свойство описываемой модели проявляется в наличии экстремальной зависимости между соотношениями массы и длины тела для заданной ЖЕЛ, которая описывается семейством парабол.

Исследуя функцию ЖЕЛ (Х₂₀) на экстремум, мы определяем, при каких сочетаниях длины тела (Х₂) и массы тела (Х₃) ЖЕЛ имеет максимальное значение для данного контингента обследуемых лиц. Дифференцируя (4) и приравнивая к нулю полученное выражение, получим уравнение линии экстремали для значений ЖЕЛ вида:

Х₂ = 2,81·Х₃. (5)

Это означает, например, что значение ЖЕЛ школьника Х₂₀ = 2,4 л при минимальном росте 146 см достигается при оптимальном значении массы тела, равном 51 кг. Линии постоянного уровня являются геометрическим местом точек, определяющим отношение между массой и длиной тела, при которых ЖЕЛ остается постоянной.

На рис.11 в трехмерной системе координат представлена поверхность отклика Х₂₀ = F(Х₂, Х₃). Рассматривая эту поверхность, видим, что каждому значению длины тела соответствует оптимальное значение массы тела, составляющее максимальное значение ЖЕЛ. Уменьшение или увеличение массы тела при заданном значении его длины уменьшает значение ЖЕЛ.

Аналогичным образом были разработаны прогнозные модели обхватных размеров тела для девочек.

Для практического использования выведенные формулы можно представить в виде моделей гармоничности физического развития, которые подростки могут определить сами и записывать результаты в дневнике самоконтроля.

Рис. 10. Линии постоянного уровня ЖЕЛ (Х₂₀) на плоскости переменных массы тела (Х₃) и длины тела (Х₂)

Рис. 11. Прогнозная экстраполированная модель ЖЕЛ

Прогнозные модели гармоничности физического развития мальчиков 10-17 лет:

1. Обхват плеча (в расслаблении) = 0,0598 · ДТ + 0,7133 · МТ - 0,0028 · МТ · ДТ ± 1,2 см.

2. Обхват бедра = 0,1453 · ДТ + 1,0155 · МТ - 0,0039 · ДТ · МТ ± 2 см.

3. Обхват талии = 0,0012 · ДТ² + 2,5543 · МТ - 0,0117 · ДТ · МТ ± 3 см.

4. Сила кисти = 0,2115 · ДТ + 0,2602 · МТ - 0,1658 · ОТ ± 3 см.

5. ОГК = 0,01 · ДТ +84,7 ± 2,5 см,

где: ДТ - длина тела, см;

МТ - масса тела, кг;

ОТ - обхват талии, см.

Прогнозные модели гармоничности физического развития девочек 10-17 лет:

1. Обхват плеча (в расслаблении) = 0,1749 · ДТ - 5,7073 ±1,2 см.

2. Обхват бедра = 0,457 · ДТ - 24,81 ±2 см.

3. Обхват талии = 0,3204 · ДТ + 12,09 ±3 см.

4. Масса тела = 0,8008 · ДТ - 78,509 ±4 кг.

5. Сила кисти = 0,3158 · МТ +4,5448 ±3 кг.

6. ОГК = 0,16 · ДТ + 62,0 ± 2,5 см.

Использованый в наших исследованиях подход, в основе которого лежит выделение факторов физического развития, имеющих функциональную взаимосвязь с показателями здоровья, дает возможность построить модели гармоничного физического развития, которые могут служить ориентиром при выборе средств физического воспитания подростков, а также использоваться в системе педагогического контроля.

Литература

1. Ареф'єв В.Г. Сучасні стандарти фізичного розвитку школярів. - Київ: Вежа, 1999. - 256 с.

2. Башкиров П.Н. Учение о физическом развитии человека. - М.: МГУ, 1962. - 340 с.

3. Гигиена детей и подростков /Под ред. Г.Н. Сердюковской. - М.: Медицина, 1989. - 319 с.

4. Детская спортивная медицина /Под ред. С.Б. Тихвинского, С.В. Хрущева. - М.: Медицина, 1991. - 547 с.

5. Круцевич Т.Ю. Методы исследования индивидуального здоровья детей и подростков в процессе физического воспитания. - Киев: Олимпийская литература, 1999. - 230 с.

6. Куц А.С. Модельные показатели физического развития и двигательной подготовленности населения центральной зоны Украины. - Киев: Искра, 1994. - 253 с.

7. Маленков В.Ф. Регрессионно-корреляционный анализ некоторых антропометрических показателей мужского населения Алтайского края /Тез. докл. науч. конф. молод. ученых и спец. антропологов Алтайского края. - Барнаул, 1987. - 20 с.

8. Физическое тестирование спортсменов высокого класса /Под ред. Дж. Дункана и др. - Киев: Олимпийская литература, 1998. - 431 с.

  На главную    В библиотеку    Обсудить в форуме 

При любом использовании данного материала ссылка на журнал обязательна!
 

Реклама: