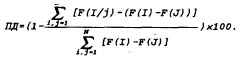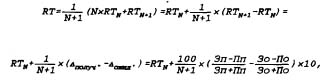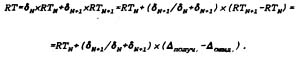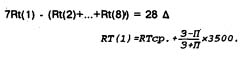ЧИТАТЕЛЬ РАЗМЫШЛЯЕТ, СПОРИТ, ПРЕДЛАГАЕТ

Polozov A.A.

Key words: macrotournament rating, participant.

РЕЙТИНГ-ФОРМУЛА

Д.Д. Полозов, Екатеринбург

Ключевые слова: макротурнир, рейтинг, участник.

Назовем рейтингом смещенный в область целых положительных чисел средний уровень результатов участника всеобщего гипотетического кругового макротурнира. Для того, чтобы не играть его на самом деле, в круг, используют принцип транзитивности: если А сильнее Б (сильнее, а не просто А выиграл у Б), а Б сильнее С, то А сильнее С. Это позволяет получать результаты макротурнира решением системы линейных уравнений методом последовательных приближений. Только макротурнир дает реальную оценку в уровне результатов. Очки - это прообраз рейтинга - тоже смещенный в область целых положительных чисел результат участника кругового микротурнира. Однако их использование приводит к огрублению результатов (три очка и за 1:0 и за 11:0), утрате большей части информации, которую потом восполняют большим числом игр. Для того чтобы продвинуться дальше, необходимо напрямую "привязаться" к результатам игр и избавиться от очкового посредника. Основной проблемой при этом является подбор вида функциональной зависимости (F). Выберем такой вид F, при котором:

1. F(3, П) = -Р(П,3), где 3,П - соответственно забитые и пропущенные голы.

2. F действует в ограниченном числовом интервале.

3. Преобразования не выходят за пределы четырех действий арифметики.

4. Предпочтение отдается той функции, при которой разница в интегральных оценках (рейтингах - Rt) двух соперников в наибольшей степени соответствует результату их личной встречи. Такой показатель назовем процентом детерминации (в дальнейшем ПД);

Далее брали произвольно турнирные таблицы из хоккея, футбола, других игровых видов спорта и выбранные из (1) виды F. Наибольшие значения ПД получила функция ("дельта") и известная таблица Эло:

Функция А все же имеет преимущество в ПД и в отличие от таблицы она представлена в аналитическом виде, а стало быть, более удобна. Рейтинг команды равен рейтингу ее соперника и на их личную встречу. При победе над соперником с Rt = 2000 П. со счетом 3:1 получаем оценку 2500. Средняя за сезон оценка является итоговой. Такое усреднение может проводиться по числу сыгранных матчей (N), а может быть пропорционально результативности этих игр. В первом случае речь идет об N-варианте, во втором - -варианте. В N-варианте:

Тогда усреднение последующего. результата с предыдущими выглядит так:

где Rt_N - средний по N последним играм Rt; ожид. - разница между Rt_N для данной команды и ее соперника. На практике более приемлемо не изменять N после каждой игры, а сразу подставлять всю сумму игр. В -варианте:

Рейтинг участника равен также сумме рейтингов соперников с удельным весом, равным результативности в личных встречах и общему по всему турниру значению .

При таком подходе полученные по (2) или (3) решением системы линейных уравнений методом последовательных приближений ("раскруткой") результаты макротурнира позволяют получать рейтинги участников, из которых можно предсказать результаты остальных несостоявшихся игр и тем самым как бы завершить макротурнир. Обязательным условием макротурнира является отсутствие в нем изолированных микротурниров. Rt, полученный решением системы линейных уравнений, может отклоняться от полученного при пересчете по (2) или (3) из-за подстановки в них текущих, а не итоговых значений Rt соперников. На практике при обычном для российских микротурниров среднем интервале между соперниками в 30-60 пунктов, отклонением в 2-3 п. можно пренебречь или решить проблему округлением последнего знака числа Rt до 0 или 5. Оба варианта совпадут, еспи игры будут проводиться до определенной суммы забитых и пропущенных голов. Например, в футболе игры могут проводиться не в течение 90 мин, а до трех забитых мячей. Для того чтобы игры не затягивались, после 90 мин игры постепенно сокращают численность игроков обеих команд. При таком подходе удается достичь большей объективности в результатах, а расчет рейтингов становится особенно прост. М-вариант кажется частным случаем -варианта. В обоих предлагаемых вариантах неизбежно возникнут искажения, если учесть хотя бы одну встречу соперников с разницей в Rt более 1000 пунктов. Такие результаты не учитываются.

Однако с практической точки зрения получение результатов через компьютер может оказаться неприемлемым. Организационно более приемлемо проведение 'макротурнира по рейтинг-формуле (РФ). Она подобна швейцарской системе. В РФ участники играют на рейтинг и на каждой последующей стадии встречаются соперники с наиболее близкими показателями. На старте все равны. Каждому участнику присваивается некоторый средний Rt (например, 2000). Следующий рейтинг получают усреднением (в N-варианте) двух последних результатов. Далее встречаются соперники с наиболее близкими текущими Rt. Число игр каждого участника, необходимое для определения Rt, зависит от числа участников N и соответствует максимальному числу игр по олимпийской системе: N = (nN)/n2. Это значит, что если, например, в стране со 150-миллионным населением найдется миллион команд, желающих играть в общем турнире, то каждой из них придется сыграть по 20 игр. Количество участников (желательно) должно соответствовать числу 2ⁿ, т.е. 4, 8, 16 и т.д. Любое четное число участников можно представить в виде суммы чисел 2ⁿ. Например, число 30 - в виде суммы 8, 8, 8, 4, 2. Эти микротурниры играют в соответствии с вышесказанным, а при их слиянии оставшимся без соперника командам корректируют рейтинг по среднему для сыгравших смещению Rt. Это значит, что если 4 из 8 команд имели преимущество в среднем на 100 пунктов в играх с другой четверкой (это при равенстве рейтингов соперников перед их встречей), то соответствующая корректировка Rt распространяется также и на четыре оставшиеся команды. Таким образом производится совмещение соответствующих средних рейтингов обоих микротурниров. При этом число туров сохраняется таким же, как и для кратного 2ⁿ числа участников. Полученный на момент окончания макротурнира результат соответствует двум последним играм. Чтобы не потерять более ранние достижения, их учитывают, добавляя к Rt соперников данного участника после И туров фактические результаты и определяя средний результат по всем встречам. Исключения составляют результаты встреч между соперниками, Rt которых отличаются после И туров более чем на 1000 пунктов. Они не учитываются. РФ является наиболее рациональной, точной и динамичной формой макротурнира. Она позволяет при минимальных затратах с максимальной точностью проводить чемпионаты мира среди любого числа участников хоть ежемесячно. Она превращает в финал каждую встречу. К растянутым на сезон национальным первенствам зрительский интерес со временем теряется. Постепенно утверждаются краткосрочные макротурниры, представляющие собой фестиваль данного вида спорта с его непременными атрибутами: широкой географией участников и соответствующим зрительским ажиотажем.

Средний Rt следующего макротурнира должен отличаться от предыдущего. Спорт не стоит не месте, развивается, прогрессирует. Рейтинги участников тянутся вверх наподобие гусеницы, чередуя циклы сжатия и растяжения. Возьмем результаты только тех, кто участвовал в обоих макротурнирах. Найдем их Rtcp. Разделим их на тех, у кого рейтинг больше Rtcp. ("верхних"), и тех, у кого Rt < Rtcp. ("нижних"). Разница средних Rt для "верхних" и "нижних" - плотность результатов - искомая величина. Модуль разницы в плотности результатов двух последних макротурниров прибавляется к среднему рейтингу последнего макротурнира по его окончании с последующей корректировкой всех результатов.

Возможна такая форма макротурнира, которая позволяет, не ломая структуры игры, провести личное первенство в командных видах спорта. Это достигается изменениями в составах команд, встречающихся в микротурнире, и приблизительным решением соответствующей системы линейных уравнений. Разность команды складывается из разностей ее игроков. В результате микротурнира игроки, переходя из команды в команду, набирают разность. Необходимо найти такую рациональную форму микротурнира, чтобы игрок играл в привычном ему режиме, на привычной позиции. Проведем микротурнир в мини-футболе в следующем режиме:

4-5 мин играет, 4-5 мин отдых. Всего 7 смен. Пусть имеются игроки-нападающие: 1, 2, 3, 4 и игроки-защитники: 5, 6, 7, 8.

1. 1234/5678

2. 1256/3478

3. 1278/3456

4. 1357/2468

5. 1368/2457

6. 1458/2367

7. 1467/2358

Поступила в редакцию 30.10.95

  На главную    В библиотеку    Обсудить в форуме 

При любом использовании данного материала ссылка на журнал обязательна!
 

Реклама: