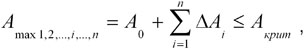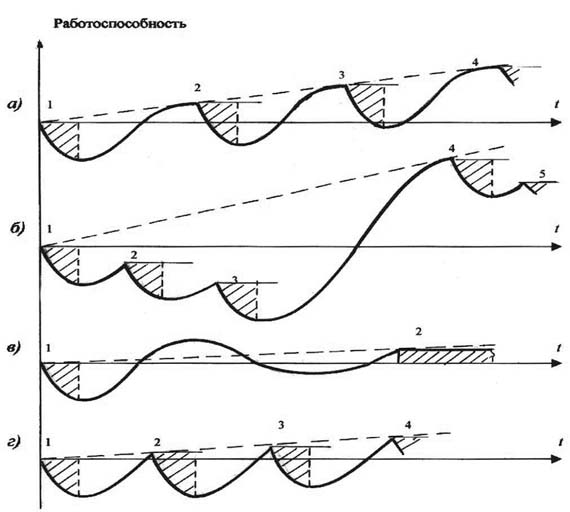
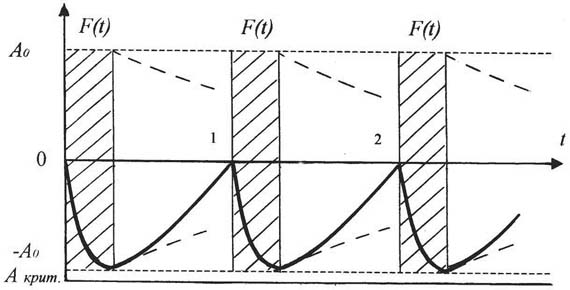
ЧЕРЕДОВАНИЕ ФИЗИЧЕСКОГО ВОЗДЕЙСТВИЯ И ОТДЫХА В СПОРТИВНОЙ ТРЕНИРОВКЕ

ЧЕРЕДОВАНИЕ ФИЗИЧЕСКОГО ВОЗДЕЙСТВИЯ И ОТДЫХА В СПОРТИВНОЙ ТРЕНИРОВКЕ

Кандидат педагогических наук, доцент А.П. Кизько

Новосибирский государственный технический университет, Новосибирск

Как известно, рациональное чередование работы и отдыха является важным фактором, определяющим эффективность спортивной тренировки. Анализ научно-методической литературы по этой тематике показал, что до настоящего времени в теории и практике спорта эта проблема не нашла однозначного решения. Выявлено, что несмотря на многообразие точек зрения на оптимальное чередование работы и отдыха, все они опираются на закон влияния физической нагрузки на организм человека, в соответствии с которым на определенном этапе восстановления, после выполнения организмом мышечной работы, запасы энергетических веществ не только достигают дорабочего уровня, но и превышают его.

Этот закон суперкомпенсации, открытый Вейгертом, был разработан школой Павлова - Фольборта применительно к вопросам рационального соотношения работы и отдыха в спортивной тренировке. В дальнейшем эти представления были неоднократно подтверждены исследованиями в лаборатории Н.Н. Яковлева. Суть этих представлений состоит в том, что каждое последующее тренировочное занятие должно возобновляться или в период "упроченного восстановления" от предшествующих занятий (по Г.В. Фольборту), или в период "повышенной работоспособности" (по Н.Н. Яковлеву), только в этом случае в результате кумуляции следовых процессов возможен высокий тренировочный эффект (рис. 1, а).

Исследования последействия тренировочных и соревновательных нагрузок, в основном по данным энергетического обмена покоя (Б.С. Гиппенрейтер, 1960; В.В. Михайлов, 1960; Л.И. Абросимов, 1959, и др.), и практика подготовки высококвалифицированных спортсменов позволили П.С. Васильеву, Н.И. Волкову (1960) предложить такой вариант чередования работы и отдыха (рис. 1, б), "при котором несколько следующих друг за другом нагрузок будут приходиться на фазу недовосстановления" функционального состояния различных органов и систем.

По их мнению, "если после этой серии нагрузок, которую можно рассматривать и как одну большую работу, дать достаточный отдых, то фаза суперкомпенсации может быть более значительной, чем после однократной нагрузки, и при правильном чередовании работы и отдыха такой вариант дает больший эффект".

В концепции спортивной тренировки Л.П. Матвеева (1965) рассматривался вариант тренировки на недовосстановлении при различном характере нагрузок и отмечалась "возможность проведения нескольких однотипных тренировочных занятий на фоне недовосстановления". Варианты соотношения работы и отдыха при различном характере нагрузки исследовались В.Н. Платоновым.

Принцип суммирования эффекта 2-3 тренировочных занятий в настоящее время находит широкое применение в технологической схеме тренировочного процесса спортсменов. В практике спорта предпринимались попытки распространить "эффект суммирования" на большое число занятий. Так, в 70-х гг. при планировании тренировки пловцов высокого класса ряд специалистов перешёл от "суммирования влияния нескольких занятий к достижению интегрального воздействия, которое является следствием выполнения на фоне недовосстановления большой работы в течение всего первого этапа подготовительного периода".

В 80-х гг. Ю.В. Верхошанский попытался теоретически обосновать эффективность принципа суммирования большого числа занятий в процессе подготовки спортсменов высокого класса преимущественно в скоростно-силовых видах спорта.

В статье Ю.П. Сергеева "О некоторых теоретических разработках и опыте внедрения в спортивную практику достижений биологической литературы" была высказана новая точка зрения на проблему оптимального соотношения работы и отдыха (рис. 1, в). По мнению автора, на определенном этапе процесса восстановления присутствует фаза, в которой для организма характерно удерживание в течение 3-4 дней "нового уровня работоспособности". В соответствии с этим была разработана технология процесса спортивной тренировки, позволявшая, по мнению разработчиков, получать необходимый для роста результатов тренировочный эффект.

Опираясь на принцип наименьшего действия (П. Мопертюн, 1946), В.В. Монахов, А.Г. Иваненко, О.В. Иванов, А.Г. Кириллов (1984) предложили "задавать тренировочную нагрузку в момент наибольшей скорости прироста работоспособности" (рис. 1, г). В серии экспериментов, проведенных авторами в группе спортсменов-гребцов, был получен положительный тренировочный эффект.

Итак, нет единства мнений. Это можно понять, если учесть, что исследователи изучали различные физические упражнения, определяли последействие неодинаковых мышечных нагрузок и использовали различные тесты. Необходимо отметить, что строгого теоретического обоснования данная проблема не нашла. Всё это порождает неоптимальные варианты решения задачи планирования чередования работы и отдыха в подготовке спортсменов.

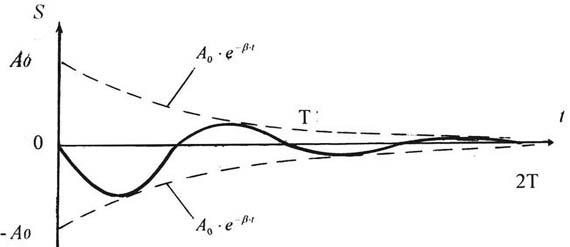
Рис. 1. Графические схемы основных вариантов чередования работы и отдыха

В этой связи целесообразно обратиться к анализу закона суперкомпенсации. Известно, что "процессы приспособления человека к любым внешним воздействиям развиваются в системе жизнеобеспечивающих ритмов, которые сами проявляются, реализуются как колебательные ритмические процессы".

Этот факт позволил нам предположить, что в колебаниях и ритмах отражается способность различных систем к развитию и самоорганизации. Для обоснования нашего предположения в качестве удобного объекта исследования рассмотрим процесс деятельности организма человека как биологической системы, о которой к настоящему времени собран богатейший фактологический материал.

Среди множества закономерностей работы организма исследователями были установлено, что внутренние показатели его работы (температура тела, давление крови, ее химический состав и др.) поддерживаются на относительно постоянном уровне. Это явление было названо гомеостазом.

В работах Н. Винера и У. Эшби были сформулированы теоретические основы функционирования гомеостатических систем. По определению названных ученых, основным свойством стабильных систем, к которым относится и организм человека, является стремление восстановить свой исходный уровень после прекращения действия возмущающего фактора. Динамика процесса восстановления функций отдельных систем и в целом всего организма отражается в законе суперкомпенсации (рис. 2).

В отечественной биологии эта закономерность достаточно полно исследована на различных уровнях организации организма в работах И.П. Павлова (1890), Г.В. Фольборта (1924, 1941, 1952), Н.Н. Яковлева (1955, 1960) и др.

С точки зрения теории колебания закон суперкомпенсации можно рассматривать как последовательное чередование двух процессов (фаз). Во-первых, на интервале времени [t₀, t₁] на систему действует вынуждающая сила и выводит ее из состояния равновесия. Во-вторых, после окончания действия вынуждающей силы на интервале времени [t₁, t₂] система совершает свободное затухающее колебание. С момента окончания свободного затухающего колебания система приходит в исходное состояние.

В реальной жизни, в частности в процессе спортивной тренировки, частота повторения физического воздействия соизмерима с длительностью фазы свободного затухающего колебания системы. В этом случае на интервале наложения (суперпозиции) колебаний система будет находиться в режиме вынужденного колебания и при некоторых условиях этот процесс может стать периодическим с определенной частотой и амплитудой колебаний, образуя ритм.

Для того чтобы показать динамику развития системы как регулярного волнового процесса (ритма), целесообразно опереться на некоторые открытые наукой факты и закономерности.

Известно, что в области пространства, где реальные колебательные системы статически (качественно) определены, по своим свойствам они достаточно близки к линейным колебательным системам. Данный факт позволяет использовать в первом приближении закономерности этих систем для дальнейшего теоретического анализа регулярного волнового процесса.

Рис. 2. Динамика восстановительного процесса в организме человека

Известно, что дифференциальное уравнение свободного затухающего колебания линейной системы имеет вид

(1)

где S - изменяющаяся при колебаниях физическая характеристика системы; b = const > 0 - коэффициент затухания колебаний системы; w₀ - циклическая частота свободного затухающего колебания той же системы, т.е. в отсутствие потерь энергии (при b = 0). Закон затухания колебаний зависит от свойств колебательной системы. Если затухание не слишком велико (b < w₀), то оно описывается уравнением

(2)

где A₀ и y₀ - постоянные величины, зависящие от начальных условий. Графически зависимость S от t при y₀= 0 показана на рис. 3.

Известно, что после приложения переменной внешней силы F (t) к системе в процессе свободного затухающего колебания на интервале взаимодействия устанавливается переходный режим вынужденных колебаний. Система одновременно участвует в двух колебаниях

(3)

Первый член уравнения соответствует свободному затухающему колебанию системы

(4)

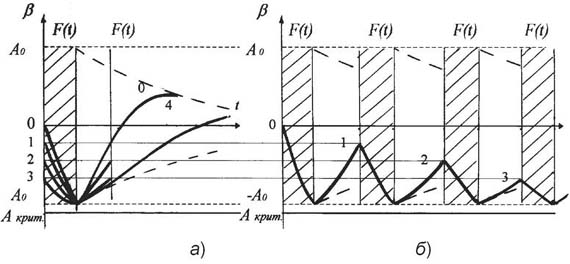
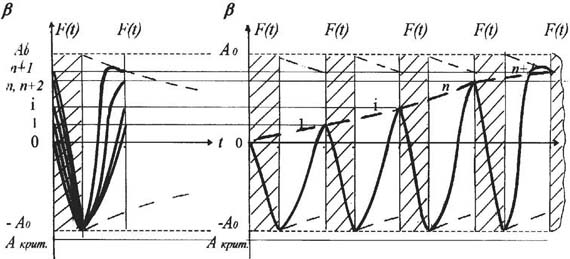
Второй член уравнения соответствует незатухающему периодическому колебанию системы с частотой, равной частоте вынуждающей силы F(t). Амплитудное значение S₁ (t), равное A₀•e^-bt, за время t₀ = 4,6/b уменьшается в 100 раз, и через некоторый промежуток времени после начала колебания (t " t₀) свободное колебание системы практически прекращается. На интервале взаимодействия система переходит в состояние установившегося вынужденного колебания, совершаемого с частотой вынуждающей силы.

Теперь рассмотрим случай, когда вынуждающая сила F(t) является периодической и при этом выполняются следующие условия:

• период колебания вынуждающей силы F(t) соизмерим с условным периодом затухающего колебания системы;

• вынуждающая сила F(t) не выводит колебательную систему за критические для нее пределы, т. е.

А_{вын. системы} < А_{критическое} .

В данном случае колебательный цикл не завершается, а система переходит в состояние регулярного волнового процесса - ритма (рис. 4).

На рис. 4 графически показан процесс последовательного формирования колебательного цикла и ритма системы при воздействии на нее на интервале [t₁, t₃] вынуждающей силы F(t) (момент времени t = t₁ выбран произвольно). До этого момента на интервале [t₀, t₁] система находилась в состоянии свободного затухающего колебания. На интервале [t₁, t₂] = t₀ система находится в состоянии вынужденного колебания. С момента t = t₃, когда с системы снимается действие вынуждающей силы, она вновь переходит в состояние свободного затухающего колебания. В момент повторного действия силы F (t), т.е. t = t₄ система завершает первый цикл колебательного процесса и начинает второй. В дальнейшем система будет находиться в состоянии ритмических колебаний определенной частоты и амплитуды.

Рис. 3. Динамика физической характеристики системы S во времени

Известно, что для простейших колебательных систем различной физической природы (пружинный маятник и электрические колебания) коэффициент затухания определяется выражением

(5) (6)

где В - коэффициент сопротивления механической среды (свойство пружины); R - коэффициент сопротивления электропроводящей среды; m - масса механической системы; L - индуктивность электропроводящей среды (характеристика, отражающая инерционные свойства этой системы).

В общем случае, опираясь на принцип подобия, можно утверждать, что коэффициент затухания колебательной системы любой физической природы есть величина, пропорциональная коэффициенту сопротивления среды, на которую воздействует вынуждающая сила, и обратно пропорциональная характеристике, связанной с инерционными свойствами системы (масса, индуктивность и т. д.), т.е.

(7)

где К - коэффициент пропорциональности; r - коэффициент сопротивления вещества физической среде; S - физическая характеристика инерционных свойств системы.

Рис. 4. Формирование колебательного цикла и ритма в процессе взаимодействия колебательной системы и вынуждающей силы (b = const)

В реальных саморегулирующихся системах коэффициент затухания в процессе взаимодействия системы с вынуждающей силой в границах колебательного цикла и ритма изменяется в некотором диапазоне. Это происходит по следующим причинам. Из области теории сопротивления материалов известно, что при увеличении нагрузки на объект коэффициент сопротивления материала нагрузке нелинейно возрастает до критических значений, за пределами которого он разрушается. Вторую причину, с нашей точки зрения, наиболее просто можно показать на примере выполнения организмом физической работы. При этом работу необходимо рассматривать как вынуждающую силу, выводящую систему из состояния равновесия. Известно, что при выполнении организмом работы расходуются его ресурсы (энергия, масса и др.), а в период восстановления организм аккумулирует ресурсы из среды. В этом процессе минимальные значения параметров системы (энергия, масса) наблюдаются в момент начала свободного затухающего колебания, а максимальные значения - через 1/2 периода свободного затухающего колебания (максимум зоны повышенной работоспособности) (см. рис. 4). Из сопоставления значений коэффициента сопротивления и параметров (энергия, масса) системы в характерных точках затухающего процесса колебания (начало и Т/2) и их взаимосвязи с коэффициентом затухания будет вытекать, что в колебательном цикле системы коэффициент затухания изменится в диапазоне от b_min до b_мах , где b_min - минимальное значение коэффициента затухания при максимальных значениях параметров системы, а b_мах - максимальное значение коэффициента затухания при минимальных значениях параметров системы.

Известно, что между коэффициентом затухания и условным периодом свободного затухания существует прямо пропорциональная зависимость, т.е. если

b₁ > b₂ >ј> b_n, то и Т₁ > Т₂ >...> Т_n.

Выше было показано, что в цикле колебания саморегулирующейся системы коэффициент затухания изменяется в диапазоне от bmin до bmaх. В этой связи очевидно, что момент приложения вынуждающей силы F (t) в каждом последующем вынужденном цикле колебания системы определяет начальную величину коэффициента затухания, с которого система начинает свое движение, и длительность условного периода свободного затухающего колебания этого цикла. Всё это существенно отражается на динамике ритма системы, и при выполнении определенных начальных условий система будет:

• во-первых, сохранять свое состояние на относительно постоянном уровне;

• во-вторых, прогрессивно развиваться в границах заложенных в эту систему возможностей;

• в-третьих, терять свою системную определенность в связи с регрессивным процессом изменения ее состояния.

На этой основе проведем анализ динамики восстановительного процесса, если частота повторения тренировочного воздействия будет совпадать с рекомендациями специалистов по чередованию работы и отдыха (см. рис. 1). Для упрощения последующего анализа примем, что амплитуда вынужденных колебаний (величина тренировочной нагрузки) системы (организм) в каждом цикле максимальна, но не превышает предельного для системы значения, т.е.

где А₀ - начальная амплитуда вынужденных колебаний, зависящая от конкретного состояния системы; i = 0, 1, 2,..., i,..., n - текущее значение колебательного цикла; DА i - изменение амплитуды вынужденных колебаний для " i " цикла; А крит - критическое отклонение параметров системы, за границей которых система разрушается.

Рассмотрим случай, когда периодическая вынуждающая сила F(t) приходится на ту часть восходящей волны затухающего процесса, когда текущие значения параметров системы не превышают их исходного уровня (рис. 5).

В нулевом цикле вынуждающая сила выводит систему из состояния равновесия. С момента повторного действия силы в фазе свободного затухающего колебания нулевого цикла система начинает первый цикл с коэффициентом затухания, равным b ₁ = b ₀ + Db _0,1.

Увеличение коэффициента затухания соответственно приводит к увеличению периода свободного затухающего колебания системы, и к началу второго цикла система переходит в новое состояние с коэффициентом, равным b ₂ = b ₁ + Db _1,2.

Процесс уменьшения амплитуды ритма и увеличения периода его колебаний будет протекать до тех пор, пока текущие значения параметров системы не достигнут критических границ для данной системы, за пределами которой она теряет свою качественную определенность (вырождается). В случае если в докритической области состояния системы снять воздействие вынуждающей силы, то система совершит свободное затухающее колебание (цикл).

Мы хотим отметить один важный результат процесса взаимодействия системы и периодической вынуждающей силы. Несмотря на то что статические характеристики системы - исходный уровень до начала взаимодействия вынуждающей силы (состояние - 0) и после ее снятия (состояние - 4) - близки по своему уровню, динамические характеристики системы в новом состоянии снижены (рис. 5, а).

Анализ динамики состояния системы, проведенный в соответствии с рекомендациями П.С. Васильева, Н.И. Волкова (1960); Л.П. Матвеева (1964) и других по чередованию работы и отдыха, позволяет констатировать, что графическая "схема расходования и восстановления энергетических потенциалов" не согласуется с теоретическими представлениями. Во-первых, отклонение параметров организма от исходного состояния при выполнении мышечной работы ограничено величиной А крит. В том случае, если каждая последующая нагрузка для организма стопроцентно развивающая, мнение специалистов, будто "чередование работы и отдыха, при котором несколько следующих друг за другом нагрузок будут приходиться на фазу недовосстановления и, суммируясь вместе, вызывать значительное снижение запасов энергетических веществ в организме", не согласуется с закономерностями формирования колебательного ритма. Во-вторых, эти специалисты утверждают, что "если после этой серии нагрузок, которую можно рассматривать и как одну большую работу, дать достаточный отдых, то фаза суперкомпенсации может быть более значительной". Однако такое мнение противоречит полученным нами теоретическим данным (см. рис 5, а, циклы 0 и 4).

Рассмотрим вариант (рис. 6), когда начало тренировочного занятия отвечает рекомендациям В.В. Монахова, А.Г. Иваненко, О.В. Иванова, А.Г. Кириллова (1984).

В нулевом цикле вынуждающая сила F(t) выводит систему из состояния равновесия. В момент повторного действия силы система начинает первый цикл с коэффициентом затухания, равным b ₁ = b ₀ .

В дальнейшем при условии точного попадания начала тренировочного занятия в точку, где наблюдается "максимальная скорость прироста работоспособности", от цикла к циклу величина коэффициента затухания будет оставаться постоянной, т.е. b ₀ = b ₁ = b _i= const, тогда Т ₀ = Т ₁ = Т _i = const.

В этой связи структура ритма системы в процессе ее взаимодействия с вынуждающей силой останется неизменной, т.е. эффект тренировочного занятия будет равен нулю. По нашему мнению, полученный этими авторами тренировочный эффект, скорее всего, связан с объективной трудностью, не позволяющей контролировать момент максимальной скорости прироста работоспособности в процессе восстановления организма.

Проанализируем на базе закономерностей теории колебаний точку зрения Ю.П. Сергеева (1980) на чередование работы и отдыха. Если величина коэффициента затухания невелика, т.е. b < w ₀,

где w ₀ - циклическая частота свободных затухающих колебаний той же системы, то в колебательном цикле системы может совершаться несколько волнообразных изменений ее состояния. При этом максимальные и минимальные значения изменений наблюдаются через промежутки времени Т, которые называются условным периодом свободного затухающего колебания. В этой связи рекомендации Ю.П. Сергеева можно рассматривать как вариант, когда величина тренировочной нагрузки и частота ее повторения будут постоянными, а начало занятия будет приходиться на максимум фазы повышенной работоспособности или на нисходящую ветвь второй волны изменения состояния организма (рис. 7).

Из рисунка видно, что в момент повторного действия силы F(t) в фазе свободного затухающего процесса нулевого цикла второй волны изменения состояния система начинает первый цикл с коэффициентом затухания, равным b ₁= b ₀ - Db _0,1.

Вследствие уменьшения коэффициента затухания и периода свободного затухающего колебания к началу второго цикла система перейдет в новое состояние. При этом в момент начала второго цикла значения параметров системы будут меньше, чем в предыдущем цикле. И система начнет второй цикл с коэффициентом затухания, равным b ₂ = b ₁ + Db _{1, 2} или b₂ = b ₀ - Db _{0, 1} + Db _{1, 2} .

Если изменения коэффициента затухания в циклах Db _{0, 1} = Db _1,
2 равны, то тогда b ₂ = b ₀ , т.е. к началу третьего цикла система перейдёт в состояние, адекватное нулевому циклу. В дальнейшем состоянии системы от цикла к циклу будут наблюдаться лишь небольшие колебания относительно первоначального. Теоретически такое состояние можно поддерживать неограниченное время.

Рис. 5. Регрессивные изменения в структуре системы: координаты начала циклов наложены друг на друга (а); колебания амплитуды ритма (б)

Рис. 6. Динамика ритма системы при наложении вынуждающей силы на момент максимальной скорости прироста параметров системы

Рис. 8. Динамика ритма системы при наложении вынуждающей силы на момент максимума зоны повышенной работоспособности

Рис. 7. Динамика ритма системы при наложении вынуждающей силы на нисходящую ветвь второй волны изменения состояния системы

Рассмотрим динамику системы, если начало физического воздействия будет приходиться на волну затухающего процесса, где текущие значения параметров системы превышают исходный уровень, что согласуется с рекомендациями Г.Ф. Фольборта, Н.Н. Яковлева и др. Из многообразия вариантов выберем тот, который соответствует моменту, когда "новая нагрузка приходится на кульминацию фазы сверхвосстановления". Для этого случая (рис. 8) в момент повторного действия силы F(t) в фазе свободного затухающего колебания нулевого цикла система начнет первый цикл с коэффициентом затухания, равным b ₁ = b ₀ - Db _{0, 1}.

Вследствие уменьшения коэффициента затухания и соответственно периода свободного затухающего колебания система перейдет к началу второго цикла в новое состояние с коэффициентом затухания, равным b ₂ = b ₁ - Db _{1, 2} .

Процесс асимптотического увеличения амплитуды ритма и уменьшения периода его колебаний будет протекать от цикла к циклу до тех пор, пока сохраняются принятые нами начальные условия, или, иными словами, если тренировочная нагрузка будет воздействовать на организм в такт ритмическим колебания его состояния.

Для этого варианта чередования работы и отдыха характерны максимальные, асимптотически нарастающие изменения в структуре ритма состояния организма. В этой связи рассмотренный вариант чередования работы и отдыха с точки зрения достижения положительного эффекта для организма спортсмена будет оптимальным.

Изложенный выше материал позволяет отметить следующую особенность волновых процессов развития, которая раскрывается в правилах планирования чередования работы и отдыха:

1. Максимальный эффект взаимосвязи работы и отдыха достигается, если новая нагрузка приходится на максимум суперкомпенсационного явления (принцип резонансного воздействия нагрузкой на организм ).

2. Эффект достигается в какой-то степени от оптимального, если новая нагрузка приходится на интервал времени от момента прихода состояния организма к "исходному" и до наступления максимума суперкомпенсации.

3. Если новая нагрузка приходится на фазу недовостановления, то, с одной стороны, в состоянии организма протекают регрессивные процессы. С другой стороны, даже при достаточном отдыхе фаза суперкомпенсации не "может быть более значительной, чем после однократной нагрузки", т.к. это противоречит законам колебательных процессов.

Вывод. Материал вносит определенную ясность в существующие представления о характере последействия тренировочных занятий на организм и позволяет с новых позиций подойти к построению оптимальной структуры чередования работы и отдыха в спортивной тренировке.

На главную В библиотеку Обсудить в форуме

При любом использовании данного материала ссылка на журнал обязательна!